Сравнение, сложение и вычитание дробей с разными знаменателями

Мы уже умеем сравнивать, складывать и вычитать дроби с одинаковыми знаменателями. Теперь рассмотрим сравнение, сложение и вычитание дробей с разными знаменателями.

Чтобы сравнить две дроби с разными знаменателями, надо:

1) привести данные дроби к общему знаменателю;

2) применить правило сравнения дробей с одинаковыми знаменателями.

Пример:

Сравним дроби .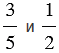

Приведем данные дроби к наименьшему общему знаменателю 10, получим:

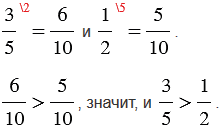
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо:

1) привести данные дроби к общему знаменателю;

2) применить правило сложения (вычитания) дробей с одинаковыми знаменателями.

Примеры:

1) Найдем сумму .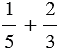

Наименьший общий знаменатель дробей 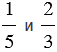равен 15. Каждую из этих дробей заменим на ей равную со знаменателем 15. Этой заменой мы сложение дробей с разными знаменателями сведем к сложению дробей с одинаковыми знаменателями, получим:

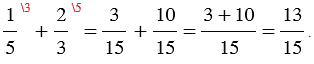
2) Найдем разность .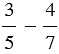

Наименьший общий знаменатель дробей 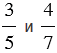равен 35. Каждую из этих дробей заменим на ей равную со знаменателем 35. Этой заменой мы вычитание дробей с разными знаменателями сведем к вычитанию дробей с одинаковыми знаменателями, получим:

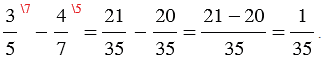
Для дробей, как и для натуральных чисел, выполняются свойства сложения:

1) Переместительное свойство: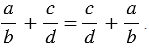

2) Сочетательное свойство: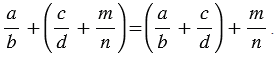

Сложение и вычитание смешанных чисел

Чтобы выполнить сложение смешанных чисел, нужно:

1) привести дробные части этих чисел к наименьшему общему знаменателю;

2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.

Пример:

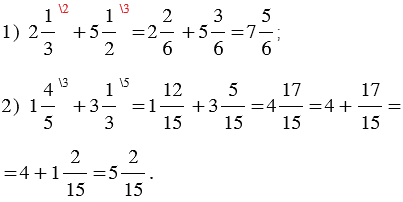
Чтобы выполнить вычитание смешанных чисел, нужно:

1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть;

2) отдельно выполнить вычитание целых частей и отдельно дробных частей.

Пример:

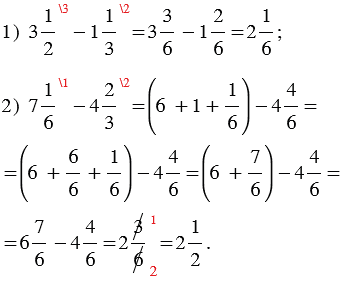
Обычно, примеры такого вида, как пример 2, записывают коротко: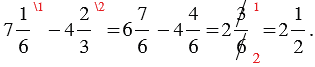

Обратите внимание: если в результате сложения или вычитания дробей получается сократимая дробь, то нужно выполнить сокращение.

Сравнение, сложение и вычитание дробей с разными знаменателями

Сложение и вычитание смешанных чисел

Советуем посмотреть:

Правило встречается в следующих упражнениях: