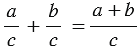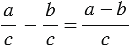Сложение и вычитание дробей с одинаковыми знаменателями
Ранее мы выполняли сложение и вычитание натуральных чисел. С дробными числами, или дробями, также можно выполнять данные действия.
Рассмотрим брусок:

Разделим его на 6 равных частей - долей:

Закрасим две доли синим цветом и три - зеленым:

То есть получим, что две шестых закрашены синим, три шестых - зеленым, а всего закрашено пять шестых:
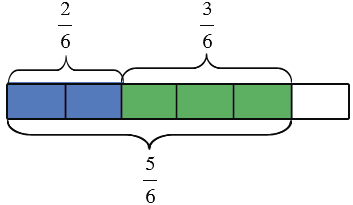
То есть мы можем сделать вывод, что:
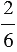 +
+ 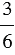 =
= 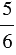 .
.
Опираясь на данный пример, можно сформулировать следующее правило:
|
Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
|
Мы знаем, что вычитание натуральных чисел определяется на основе сложения: вычесть из одного числа другое - это значит найти такое число, которое при сложении с вычитаемым дает уменьшаемое. Аналогично вычитание дробей дается на основе их сложения.
Например, рассмотрим наш брусок:

Нам известно, что на нем закрашено пять шестых частей, из которых две части синие, а остальные зеленые, нам надо найти какая часть бруска закрашена зеленым цветом:
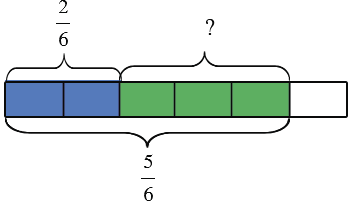
Чтобы ответить на поставленный вопрос, нам надо найти разность дробей 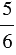 и
и 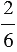 . Вычесть из дроби
. Вычесть из дроби 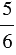 дробь
дробь 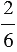 , значит найти такое число, которое в сумме с числом
, значит найти такое число, которое в сумме с числом 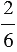 дает число
дает число 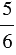 . Как было выше сказано
. Как было выше сказано 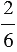 +
+ 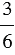 =
= 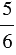 , поэтому
, поэтому 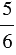 -
- 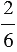 =
= 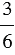 . Итак, имеем:
. Итак, имеем:
|
Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
|
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 1067, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1126, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1251, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5.286, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.396, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 16, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.85, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 1124, Мерзляк, Полонский, Якир, Учебник
Номер 1196, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 248, Мерзляк, Полонский, Якир, Учебник
Номер 287, Мерзляк, Полонский, Якир, Учебник
Номер 372, Мерзляк, Полонский, Якир, Учебник
Номер 948, Мерзляк, Полонский, Якир, Учебник
Номер 956, Мерзляк, Полонский, Якир, Учебник
Задание 914, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 3.119, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.294, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.85, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.129, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 35, Мерзляк, Полонский, Якир, Учебник
Номер 114, Мерзляк, Полонский, Якир, Учебник
Номер 115, Мерзляк, Полонский, Якир, Учебник
Номер 139, Мерзляк, Полонский, Якир, Учебник
Номер 146, Мерзляк, Полонский, Якир, Учебник
Номер 197, Мерзляк, Полонский, Якир, Учебник
Номер 348, Мерзляк, Полонский, Якир, Учебник
Номер 429, Мерзляк, Полонский, Якир, Учебник
Номер 646, Мерзляк, Полонский, Якир, Учебник
Упражнение 1195, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 66, Мерзляк, Полонский, Якир, Учебник
Номер 242, Мерзляк, Полонский, Якир, Учебник
Номер 243, Мерзляк, Полонский, Якир, Учебник
Номер 255, Мерзляк, Полонский, Якир, Учебник
Номер 872, Мерзляк, Полонский, Якир, Учебник
Упражнение 359, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 579, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1138, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1338, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 283, Макарычев, Миндюк, Учебник
9 класс