Признаки делимости на 9 и на 3
Признак делимости на 9
Задача
Разложить, не выполняя деления, 513 еловых шишек в 9 корзин поровну
Решение









В числе 513 содержится 5 сотен, 1 десяток и 3 единицы.
Если раскладывать поровну в 9 корзин одну сотню шишек, то в каждую корзину можно положить 11 шишек, а одна шишка останется.
От пяти сотен останется в 5 раз больше, то есть, 5 шишек.
Если раскладывать поровну в 9 корзин один десяток шишек, то в каждую корзину можно положить 1 шишку, а одна шишка останется.
Не разложенными в 9 корзин останутся:




 - 5 шишек от пяти сотен
- 5 шишек от пяти сотен
 - 1 шишка от десятка
- 1 шишка от десятка


 - и ещё 3 шишки
- и ещё 3 шишки
Всего останется 9 шишек
Так как 9 шишек можно разложить поровну в 9 корзин (по одной шишке в каждую), то и все 513 шишек можно разложить поровну в 9 корзин.
Значит, число 513 делится на 9 без остатка.
Определим сумму цифр в записи числа 513
5 + 1 + 3 = 9
Число 9 является суммой цифр числа 513.
Определение
Если сумма цифр числа делится на 9, то и число делится на 9;
если сумма цифр числа не делится на 9, то и число не делится на 9.
Примеры
Число 36 144 делится на 9, так как сумма его цифр: 3 + 6 + 1 + 4 + 4 = 18 - делится на 9.
Число 41 234 не делится на 9, так как сумма его цифр: 4 + 1 + 2 + 3 + 4 = 14 - не делится на 9.
Заметим, что разность между числом и суммой его цифр всегда делится на 9. Для доказательства данного факта рассмотрим произвольное четырехзначное 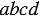 число, данное число содержит
число, данное число содержит 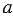 - тысяч,
- тысяч, 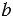 - сотен,
- сотен, 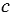 - десятков и
- десятков и  - единиц. То есть
- единиц. То есть 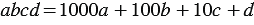 , тогда сумма его цифр равна
, тогда сумма его цифр равна  . Найдем разность полученных сумм, получим:
. Найдем разность полученных сумм, получим:
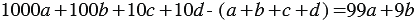
Очевидно, что слагаемые полученной суммы делятся на 9, а значит, и сумма делится на 9, то есть разность между числом и суммой его цифр делится на 9. Аналогично можно провести доказательство для любого числа.
Признак делимости на 3
Так же обосновывается признак делимости на 3.
Задача
Разложить 126 шишек на 3 кучки поровну



Решение
В числе 126 содержится 1 сотня, 2 десятка и 6 единиц
Если раскладывать поровну на три кучки одну сотню шишек, то в каждую кучку можно положить 33 шишки, а одна шишка останется.
Если раскладывать поровну на три кучки один десяток шишек, то в каждую кучку можно положить 3 шишки, а одна шишка останется.
От двух десятков останется 2 шишки.
Шесть шишек можно разложить на три кучки по две шишки
Не разложенными по трем кучкам останутся: 1 шишка от одной сотни, 2 шишки от двух десятков
 - 1 шишка от одной сотни
- 1 шишка от одной сотни

 - 2 шишки от двух десятков
- 2 шишки от двух десятков
Всего останется 3 шишки
Так как 3 шишки можно разложить поровну на три кучки (по одной шишке в каждую), то и все 126 шишек можно разложить поровну на три кучки.
Значит, число 126 делится на 3 без остатка.
Определим сумму цифр в записи числа 126
1 + 2 + 6 = 9
Число 9 является суммой цифр числа 126.
Определение
Если сумма цифр числа делится на 3, то и число делится на 3;
если сумма цифр числа не делится на 3, то и число не делится на 3.
Примеры
Число 3744 делится на 3, так как сумма его цифр: 3 + 7 + 4 + 4 = 18 - делится на 3.
Число 1534 не делится на 3, так как сумма его цифр: 1 + 5 + 3 + 4 = 13 - не делится на 3.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание П.11, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 3.381, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.382, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.383, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.389, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.391, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.423, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.424, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.425, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание Проверочная работа №2, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
6 класс
Номер 73, Мерзляк, Полонский, Якир, Учебник
Номер 83, Мерзляк, Полонский, Якир, Учебник
Номер 86, Мерзляк, Полонский, Якир, Учебник
Номер 157, Мерзляк, Полонский, Якир, Учебник
Задание 62, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 117, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 243, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 915, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 10, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 128, Мерзляк, Полонский, Якир, Учебник
Номер 131, Мерзляк, Полонский, Якир, Учебник
Номер 195, Мерзляк, Полонский, Якир, Учебник
Номер 196, Мерзляк, Полонский, Якир, Учебник
Номер 289, Мерзляк, Полонский, Якир, Учебник
Номер 354, Мерзляк, Полонский, Якир, Учебник
Упражнение 12, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 13, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 520, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1210, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 26, Мерзляк, Полонский, Якир, Учебник
Номер 801, Мерзляк, Полонский, Якир, Учебник
Упражнение 396, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 397, Макарычев, Миндюк, Нешков, Суворова, Учебник