Упражнение 699 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\[ \begin{cases} x^{2}-4=0,\\ y^2-9=0 \end{cases} \]

\[ \begin{cases} x^{2}=4,\\ y^2=9 \end{cases} \]

\[ \begin{cases} x=2 \;\; или \;\; x = -2,\\ y=3 \;\; или \;\; y = -3 \end{cases} \]

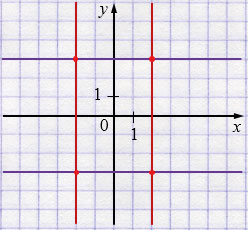
Ответ: \((-2; \; 3)\), \((2; \; 3)\),

\((2; \; -3)\), \((-2; \; -3)\).

Пояснения:

Суть графического метода решения системы уравнений с двумя переменными:

1) построить на одной координатной плоскости графики уравнений, входящих в систему;

2) найти координаты всех точек пересечения построенных графиков;

3) полученные пары чисел и будут искомыми решениями.

В каждом уравнении системы выражаем квадрат переменной, получаем уравнения вида \(x^2 = a\) и \(y^2 = b\), каждое из этих уравнений имеет два решения \(x = \pm2\) и \(y = \pm3\).

Графиком функции \(x = a\) является прямая, параллельная оси \(y\) и проходящая через точку \(a; 0\).

Графиком функции \(y = b\) является прямая, параллельная оси \(x\) и проходящая через точку \(0; b\).

Графики уравнений системы пересеклись в четырех точках, значит, рассматриваемая система имеет 4 решения.

\(30 \; мин = \frac12 \; ч\)

Составим уравнение:

\(\frac{18}{x+1} + \frac12 = \frac{14}{x-1}\)  \(/\times2(x+1)(x-1)\)

ОДЗ: \(x+1\neq0\)   и   \(x - 1 \neq0\)

         \(x\neq-1\)            \(x\neq1\)

\(36(x-1) +(x+1)(x-1) = 28(x+1)\)

\(36x - 36 + x^2 - 1 = 28x+28\)

\(36x - 36 + x^2 - 1 - 28x-28 = 0\)

\(x^2 +8x -65 = 0\)

\(a = 1\),  \(b = 8\),  \(c = -65\)

\(D = b^2 - 4ac = 8^2 - 4\cdot1\cdot(-65)=\)

\(=64 + 260 = 324\),    \(\sqrt D = 18\).

\(x_1 = \frac{-8+18}{2\cdot1} = \frac{10}{2} = 5\).

\(x_2 = \frac{-8-18}{2\cdot1} = \frac{-26}{2} = -13\) - не удовлетворяет условию.

1) \(5\) км/ч - скорость на первом переходе.

2) \(\frac{12,5}{5} = 2,5\) (ч) - время на первый переход.

3) \(\frac{18}{5 + 1} = \frac{18}{6} = 3\) (ч) - время на второй переход.

4) \(\frac{14}{5 - 1} = \frac{14}{4} = 3,5\) (ч) - время на третий переход.

5) \(2,5 + 3 + 3,5 = 9\) (ч)

Ответ: все переходы заняли \(9\) ч.

Пояснения:

Время в пути вычисляется по формуле \[t=\frac{S}{v}.\]

Скорость на первом переходе обозначили \(x\) км/ч, по условию задачи составили дробное рациональное уравнение:

\(\frac{18}{x+1} + \frac12 = \frac{14}{x-1}\).

Алгоритм решения дробного рационального уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили полное квадратное уравнение, у которого дискриминант \(D = b^2 - 4ac>0\), поэтому уравнение имеет два корня: \(5\) и \(-13\). Но отрицательный корень не подходит, так как скорость не может быть отрицательным числом. Значит, скорость на первом переходе равна \(5\) км/ч.

Учитывая обозначения, определили время на втором и третьем переходах, затем нашли общее время на всех переходах.