Упражнение 698 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 149
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№698 учебника 2023-2025 (стр. 149):
Замените степень произведением, а затем произведение преобразуйте в многочлен:
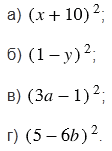
№698 учебника 2013-2022 (стр. 149):
Найдите корень уравнения:
а) \(5 + x^2 = (x+1)(x+6);\)
б) \(2x(x - 8) = (x + 1)(2x - 3);\)
в) \((3x - 2)(x + 4) - 3(x + 5)(x - 1) = 0;\)
г) \(x^2 + x(6 - 2x) = (x - 1)(2 - x) - 2.\)
Подсказка
№698 учебника 2023-2025 (стр. 149):
Вспомните:
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Что называют многочленом.
- Умножение многочлена на многочлен.
- Умножение рациональных чисел.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
№698 учебника 2013-2022 (стр. 149):
Вспомните:
- Что значит решить уравнение.
- Линейное уравнение.
- Деление и дроби.
- Неправильные дроби.
- Смешанные числа.
- Сокращение дробей.
- Деление десятичных дробей.
- Свойства уравнений.
- Умножение многочлена на многочлен.
- Сложение и вычитание многочленов.
- Умножение рациональных чисел.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Распределительное свойство умножения.
Ответ
№698 учебника 2023-2025 (стр. 149):
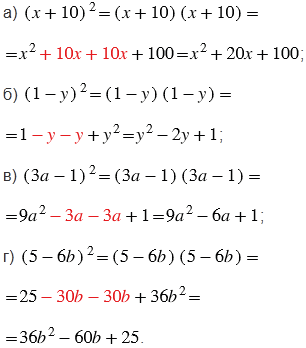
Пояснения:
Учитывая определение степени, представляем многочлен данный в квадрате в виде произведения двух таких многочленов и выполняем умножение многочлена на многочлен.
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить (мы говорим об алгебраической сумме - выражение, которое можно представить в виде суммы положительных и отрицательных чисел). В решении выделены одинаковым цветом подобные слагаемые, их мы складываем (вычитаем), тем самым упрощая выражение.
№698 учебника 2013-2022 (стр. 149):
Решение:
а) \(5 + x^2 = (x+1)(x+6) \)
\(5 + x^2 =x^2 + 6x +x + 6\)
\(5 + x^2 =x^2 + 7x + 6\)
\(x^2 -x^2 -7x = 6 -5 \)
\(-7x= 1\)
\(x = -\frac{1}{7}\)
Ответ: \(x = -\frac{1}{7}\).
б) \(2x(x - 8) = (x + 1)(2x - 3);\)
\(2x^2 - 16x = 2x^2 - 3x +2x - 3\)
\(2x^2 - 16x = 2x^2 - x - 3\)
\(2x^2 -2x^2 -16x + x = -3\)
\(-15x = -3\)
\(x=\frac{\cancel3^{1}}{\cancel{15}_{5}}\)
\(x = \frac{1}{5}\)
Ответ: \(x = \frac{1}{5}\).
в) \((3x - 2)(x + 4) - 3(x + 5)(x - 1) = 0;\)
\(3x^2 + 12x -2x - 8 - 3(x^2 -x +5x - 5) =0\)
\(3x^2 + 10x - 8 - 3(x^2 +4x - 5) =0\)
\(3x^2 + 10x - 8 - 3x^2 -12x + 15 =0\)
\(-2x + 7 = 0\)
\(-2x = -7\)
\(x = \frac{7}{2}\)
\(x = 3,5\)
Ответ: \(x = 3,5\).
г) \(x^2 + x(6 - 2x) = (x - 1)(2 - x) - 2\)
\(x^2 + 6x - 2x^2 = 2x - x^2 - 2 +x -2\)
\(-x^2 + 6x = -x^2 +3x -4\)
\(-x^2 +x^2 +6x -3x = -4\)
\(3x = -4\)
\(x = -\frac{4}{3}\)
\(x = -1\frac{1}{3}\)
Ответ: \(x = -1\frac{1}{3}\).
Пояснения:
Использованные правила:
1. Раскрытие произведения скобок:
\((a+b)(c+d)=ac+ad+bc+bd\).
2. Распределительное свойство умножения (раскрытие скобок):
\(x(y+z)=xy+xz\).
3. Вычитание многочленов: чтобы вычесть \((P(x) - Q(x))\), меняем знак у всех членов \(Q(x)\) и складываем с \(P(x)\).
4. Приведение подобных членов:
\(ax^2 + bx + cx^2 = (a+c)x^2 + bx\).
5. Перенос членов через знак «=»: если
\(A + C= B + D\), то
\(A - D = B - C\).
6. Решение линейного уравнения:
из \(ax = b\) следует \(x = \tfrac{b}{a}\) при \(a\neq0\).
Пояснение к пункту а):
Раскрыли скобки в правой части:
\((x+1)(x+6)=x^2+7x+6\). Затем перенесли \(x^2\) и \(7x\) из правой в левую часть, сократили противоположные выражения и привели подобные, решили линейное уравнение \(-7x= 1\).
Пояснение к пункту б):
Раскрыли скобки в левой части:
\(2x(x-8)=2x^2-16x\)
и в правой части:
\((x+1)(2x-3)=2x^2-x-3\).
Затем перенесли \(2x^2\) и \(-x\) из правой в левую часть, сократили противоположные выражения и привели подобные, решили линейное уравнение \(-15x = -3\).
Пояснение к пункту в):
Сначала раскрыли обе пары скобок, затем выполнили вычитание многочленов:
\( (3x^2+10x-8)-(3x^2+12x-15)= -2x+7\),
Сократили противоположные выражения и привели подобные, перенесли выражения без переменной из левой части уравнения в правую, решили линейное уравнение \(-2x = -7\).
Пояснение к пункту г):
Упростили левую часть:
\(x^2+x(6-2x)=x^2+6x-2x^2=-x^2+6x\).
Правую часть:
\((x-1)(2-x)-2=-x^2+3x-4\).
Перенесли выражения с переменной из правой части уравнения в левую, а без переменной - из левой части уравнения в правую, сократили противоположные выражения и привели подобные, решили линейное уравнение \(3x = -4\).
Вернуться к содержанию учебника