Теорема Виета
Теорема Виета
|
Если
|
Доказательство:
Так как условие теоремы предполагает, что данное квадратное уравнение имеет корни, то его дискриминант  не может быть отрицательным. Пусть
не может быть отрицательным. Пусть  >0. Применив формулу корней квадратного уравнения, мы можем записать:
>0. Применив формулу корней квадратного уравнения, мы можем записать:

Имеем:

Пусть  =0. В этом случае, считают, что
=0. В этом случае, считают, что  имеем:
имеем:


Следствие
|
Если
|
То есть: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Заметим, что в некоторых источниках именно эту формулировку принимают за теорему Виета.
Теорема, обратная теореме Виета
Если числа  и и  таковы, что таковы, что 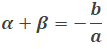 и и  , то эти числа являются корнями квадратного уравнения , то эти числа являются корнями квадратного уравнения  . . |
Доказательство:
Рассмотрим квадратное уравнение  Преобразуем его в приведенное:
Преобразуем его в приведенное:

Согласно условию теоремы это уравнение можно записать так:

Подставим в левую часть уравнения вместо  сначала число
сначала число  , затем число
, затем число  . Получим:
. Получим:

Таким образом, числа  и
и  являются корнями уравнения (*), а следовательно, и корнями квадратного уравнения
являются корнями уравнения (*), а следовательно, и корнями квадратного уравнения 
Следствие
Если числа  и и  таковы, что таковы, что  и и  , то эти числа являются корнями приведённого квадратного уравнения , то эти числа являются корнями приведённого квадратного уравнения  . . |
Советуем посмотреть:
Квадратные уравнения. Решение неполных квадратных уравнений.
Формула корней квадратного уравнения
Решение уравнений, сводящихся к квадратным уравнениям
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 708, Мерзляк, Полонский, Якир, Учебник
Номер 744, Мерзляк, Полонский, Якир, Учебник
Номер 746, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
Номер 759, Мерзляк, Полонский, Якир, Учебник
Номер 788, Мерзляк, Полонский, Якир, Учебник
Номер 793, Мерзляк, Полонский, Якир, Учебник
Упражнение 739, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 779, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс
 и
и  -
- 
