Окружность, круг, шар

Окружность - это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О - центр окружности.

Основные характеристики окружности

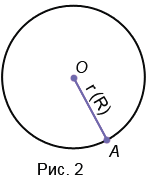
1. Радиус - это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.

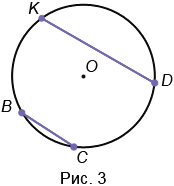
2. Хорда - это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD - хорды окружности с центром в точке О.

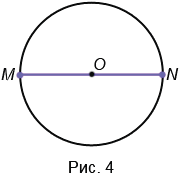
3. Диаметр - это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр - это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN - диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.

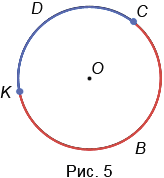
4. Дуга - это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC - дуги, ограниченные точками К и С.

Построение окружности

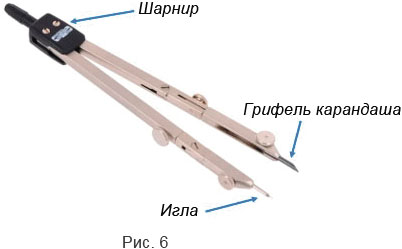
Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.

Выполнение построения:

• отмечаем точку, которая будет центром окружности;
• делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);

• ставим иглу циркуля в точку, которая определяет центр окружности;
• проводим окружность данного радиуса (Рис.8).

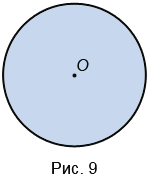
Часть плоскости, которая лежит внутри окружности (вместе с самой окружностью), называют кругом (Рис.9).

Часть круга, ограниченную двумя радиусами называют сектором, на рисунке 10 два сектора.

Шар и сфера

Сфера - поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

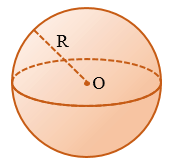
Центр сферы - данная точка (точка О на рисунке выше).

Радиус сферы - данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий центр сферы с какой-либо ее точкой.

Диаметр сферы - отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы - R, то ее диаметр - 2R.

Определение