Объем прямоугольного параллелепипеда
Каждое из рассматриваемых нами тел имеет объём, который можно измерить с помощью выбранной единицы измерения объёмов. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Такой куб называют единичным (смотри рисунок ниже).
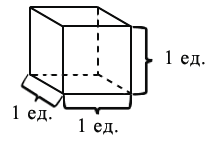
Единицы измерения объема:
| Ребро куба | Название объема куба | Запись объема |
| 1 мм | кубический миллиметр | 1 мм3 |
| 1 см | кубический сантиметр | 1 см3 |
| 1 дм | кубический дециметр | 1 дм3 |
| 1 м | кубический метр | 1 м3 |
| 1 км | кубический километр | 1 км3 |
При измерении объемов жидкостей или газов 1 дм3 называют литром, и записывают так: 1 л = 1 дм3.
Обозначают объем буквой 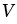 , т.е. если нам сказано, что объем фигуры равен 24 см3, то это можно записать так:
, т.е. если нам сказано, что объем фигуры равен 24 см3, то это можно записать так: 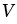 = 24 см3.
= 24 см3.
| Измерить объем фигуры - значит подсчитать, сколько единичных кубов в ней помещается. |
Свойства объемов
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
Формула для вычисления объема прямоугольного параллелепипеда
| Объем прямоугольного параллелепипеда равен произведению трех его измерений: длины, ширины и высоты. |
Если 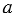 - длина параллелепипеда,
- длина параллелепипеда, 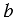 - ширина параллелепипеда,
- ширина параллелепипеда, 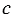 - высота параллелепипеда, то объем такого параллелепипеда будет выражаться формулой:
- высота параллелепипеда, то объем такого параллелепипеда будет выражаться формулой: 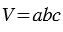 .
.
Пример:
Найдем объем 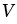 параллелепипеда с ребрами 5 см, 2 см и 8 см:
параллелепипеда с ребрами 5 см, 2 см и 8 см:
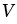 = 5
= 5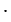 2
2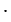 8 = 80 (см3).
8 = 80 (см3).
Связь объема параллелепипеда с площадью его основания
Если 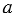 - длина прямоугольного параллелепипеда,
- длина прямоугольного параллелепипеда, 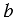 - его ширина, то их произведение равно площади
- его ширина, то их произведение равно площади 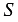 основания рассматриваемого параллелепипеда, т.к. основанием прямоугольного параллелепипеда является прямоугольник, т.е.
основания рассматриваемого параллелепипеда, т.к. основанием прямоугольного параллелепипеда является прямоугольник, т.е. 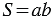 (смотри рисунок ниже).
(смотри рисунок ниже).
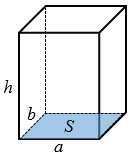
Если высоту данного прямоугольного параллелепипеда обозначить буквой 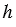 , тогда объем данного параллелепипеда будет равен
, тогда объем данного параллелепипеда будет равен 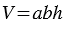 , откуда, учитывая то, что
, откуда, учитывая то, что 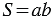 , получим:
, получим: 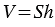 .
.
| Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. |
Пример:
Найдем объем 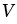 прямоугольного параллелепипеда, площадь основания которого равна 20 см2, а высота равна 7 см:
прямоугольного параллелепипеда, площадь основания которого равна 20 см2, а высота равна 7 см:
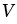 = 20
= 20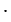 7 = 140 (см3).
7 = 140 (см3).
Формула для вычисления объема куба
У куба все ребра равны, т.е. длина, ширина и высота совпадают, тогда, если ребро куба 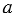 , его объем будет вычисляться по формуле:
, его объем будет вычисляться по формуле: 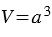 .
.
Пример:
Найдем объем 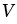 куба с ребром 3 дм:
куба с ребром 3 дм:
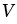 = 33 = 3
= 33 = 3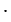 3
3 3 = 27 (дм3).
3 = 27 (дм3).
Связь между метрическими единицами объема
1 м3 = 1 000 дм3 = 103 дм3
1 дм3 = 1 000 см3 = 103 см3
1 см3 = 1 000 мм3 = 103 мм3
1 км3 = 1 000 м 1 000 м
1 000 м 1 000 = 109 м3.
1 000 = 109 м3.
Советуем посмотреть:
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Прямоугольный параллелепипед. Пирамида.
Измерение углов. Транспортир. Виды углов
Правило встречается в следующих упражнениях:
5 класс
Задание 819, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1805, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание П.66, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.105, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.155, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 625, Мерзляк, Полонский, Якир, Учебник
Номер 637, Мерзляк, Полонский, Якир, Учебник
Номер 954, Мерзляк, Полонский, Якир, Учебник
Номер 1203, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 365, Мерзляк, Полонский, Якир, Учебник
Номер 514, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Задание 750, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 782, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 991, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1036, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1.157, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.273, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание Проверочная работа №2, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 230, Мерзляк, Полонский, Якир, Учебник
Номер 757, Мерзляк, Полонский, Якир, Учебник
Упражнение 50, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 192, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 260, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 448, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 450, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 477, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 296, Мерзляк, Полонский, Якир, Учебник
Номер 316, Мерзляк, Полонский, Якир, Учебник
Упражнение 192, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 384, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 760, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 965, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1231, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс