Упражнение 716 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№716 учебника 2023-2025 (стр. 169):
Построив схематически графики уравнений, выясните, сколько решений имеет система уравнений:
а) \(\begin{cases} y=x^3, \\ y=15x; \end{cases}\)
б) \(\begin{cases} xy=10, \\ y=x. \end{cases}\)
№716 учебника 2013-2022 (стр. 158):
Бригада рабочих должна была за определённый срок изготовить 768 пылесосов. Первые 5 дней бригада выполняла ежедневно установленную норму, а затем каждый день изготавливала на 6 пылесосов больше, чем намечалось, поэтому уже за день до срока было изготовлено 844 пылесоса. Сколько пылесосов в день должна была изготавливать бригада по плану?
Подсказка
№716 учебника 2023-2025 (стр. 169):
Вспомните:
- Графический способ решения систем уравнений.
- Координаты точки.
- График кубической параболы.
- График обратной пропорциональности.
- Линейная функция, ее график.
№716 учебника 2013-2022 (стр. 158):
Вспомните.
- Решение дробных рациональных уравнений.
- Рациональные дроби.
- Основное свойство рациональной дроби.
- Полные квадратные уравнения (упрощенный дискриминант).
- Арифметический квадратный корень.
- Подобные слагаемые.
- Свойства уравнений.
- Умножение одночлена на многочлен.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
Ответ
№716 учебника 2023-2025 (стр. 169):
а) \( \begin{cases} y=x^3, \\ y = 15x \end{cases} \)
\( y=x^3\) - кубическая парабола, I и III четверть.
\(y = 15x\) - возрастающая прямая, проходит через точку \((0;0)\).

Ответ: система имеет 3 решения.
б) \( \begin{cases} xy=10, \\ y = x \end{cases} \)
\( \begin{cases} y=\frac{10}{x}, \\ y = x \end{cases} \)
\(y=\frac{10}{x}\) - гипербола, I и III четверть.
\(y=x\) - возрастающая прямая, проходит через точку \((0;0)\).
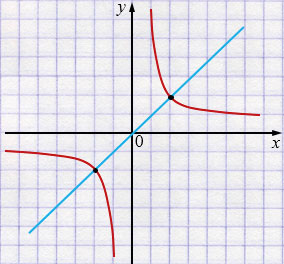
Ответ: система имеет 2 решения.
Пояснения:
Суть графического метода решения системы уравнений с двумя переменными:
1) построить на одной координатной плоскости графики уравнений, входящих в систему;
2) найти координаты всех точек пересечения построенных графиков;
3) полученные пары чисел и будут искомыми решениями.
а) График \(y=x^3\) — кубическая парабола, а \(y=15x\) — прямая через начало координат. Они пересекаются в трёх точках, что соответствует трём решениям.
б) График \(xy=10\) — гипербола, а \(y=x\) — прямая, которая является биссектрисой угла между осями. Они пересекаются в двух точках, что соответствует двум решениям.
№716 учебника 2013-2022 (стр. 158):
Пусть по плану бригада должна была изготавливать \(x\) пылесосов в день, тогда плановый срок работы: \(\frac{768}{x}\).
За первые 5 дней бригада изготовила: \(5x\) пылесосов, тогда за оставшиеся дни она изготовила \(844 - 5x\), изготавливая в день по \(x + 6\) пылесосов.
Составим уравнение:
\(\frac{768}{x} = 5 + \frac{844 - 5x}{x + 6} + 1\)
\(\frac{768}{x} = 6 + \frac{844 - 5x}{x + 6}\) \(/\times x(x+6)\)
ОДЗ: \(x\neq0\) и \(x + 6\neq 0\)
\(x\neq-6\)
\(768(x + 6) = 6x(x+6) + x(844 - 5x) \)
\(768x + 4608 = 6x^2 + 36x + 844x -5x^2\)
\(768x + 4608 = x^2 + 880x\)
\(x^2 + 880x -768x - 4608 = 0\)
\(x^2 + 112x - 4608=0\)
\(a = 1\), \(k = \frac b2 = 56\), \(c = -4608\)
\(D_1 = k^2 - ac =\)
\(=56^2 -1\cdot(-4608)=\)
\(=3136 + 4608 = 7744\), \(\sqrt D = 88\).
\(x_{1,2} = \frac{-k \pm \sqrt D}{a}\)
\(x_1 = \frac{-56 + 88}{1} = 32\)
\(x_2 = \frac{-56 - 88}{1} = -144\) - не удовлетворяет условию.
Ответ: по плану бригада должна была изготавливать \(32\) пылесоса в день.
Пояснения:
Обозначили плановую дневную норму за \(x\). Определили плановый срок как \(\frac{768}{x}\) дней.
Составили дробное рациональное уравнение, учитывая то, что сначала 5 дней бригада работала по плану, затем каждый день изготавливала на 6 пылесосов больше: больше, при этом за день до срока было изготовлено 844 пылесоса:
\(\frac{768}{x} = 5 + \frac{844 - 5x}{x + 6} + 1\).
Алгоритм решения дробного рационального уравнений:
1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;
2) найти общий знаменатель дробей, входящих в уравнение;
3) умножить обе части уравнения на общий знаменатель;
4) решить получившееся целое уравнение;
5) исключить из его корней те, которые совпадают с ОДЗ.
После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение с четным коэффициентом \(b\), у которого дискриминант \(D_1 = k^2 - 4ac>0\), где \(k = \frac b2\), поэтому уравнение имеет два корня: \(32\) и \(-144\). Корень, равный \-144\), не удовлетворяет условию задачи, так как количество не может быть отрицательным числом.
Значит, по плану бригада должна была изготавливать \(32\) пылесоса в день.
Вернуться к содержанию учебника