Упражнение 675 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№675 учебника 2023-2025 (стр. 158):
Постройте график уравнения:
а) \(3x+0y=12\);
б) \(0x+y=1\);
в) \(x=5\);
г) \(y=1{,}5\);
д) \((x-2)(y-3)=0\);
е) \((x+3)(y+1)=0\);
ж) \(|x|=2\);
з) \(|y|=3\).
№675 учебника 2013-2022 (стр. 154):
Докажите, что если сумма коэффициентов квадратного уравнения \[ax^2 + bx + c = 0\] равна нулю, то один из корней уравнения равен 1. Используя это свойство, решите уравнение:
а) \(2x^2 - 41x + 39 = 0\);
б) \(17x^2 + 243x - 260 = 0\).
Подсказка
№675 учебника 2023-2025 (стр. 158):
Вспомните:
- Линейное уравнение с двумя переменными, его график.
- Координаты точки.
- Параллельные прямые.
- Модуль числа.
- Свойства умножения.
- График линейной функции.
№675 учебника 2013-2022 (стр. 154):
Вспомните:
- Решение полных квадратных уравнений (дискриминант).
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Степень с натуральным показателем.
- Модуль числа.
- Деление и дроби.
- Противоположные числа.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Умножение рациональных чисел.
- Сокращение дробей.
- Неправильные дроби.
- Смешанные числа.
Ответ
№675 учебника 2023-2025 (стр. 158):
а) \(3x+0y=12\)
\(3x=12\)
\(x=4\)
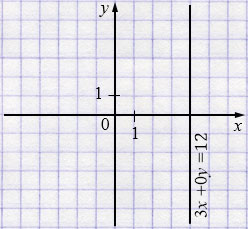
б) \(0x+y=1\)
\(y=1\)
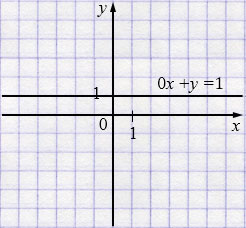
в) \(x=5\)
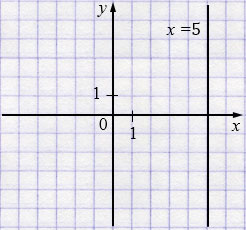
г) \(y=1{,}5\)
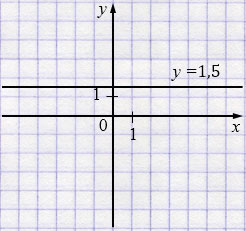
д) \((x-2)(y-3)=0\)
\(x - 2 = 0\) или \(y - 3 = 0\)
\(x=2\) \( y=3\)
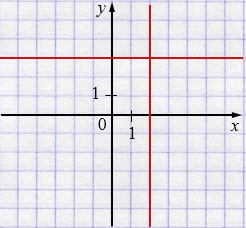
е) \((x+3)(y+1)=0\)
\(x+3 = 0\) или \(y + 1 = 0\)
\(x=-3\) \( y=-1\)
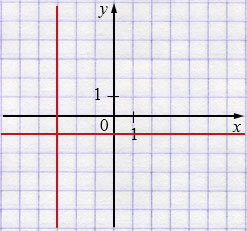
ж) \(|x|=2\)
\(x=2\) или \( x=-2\)
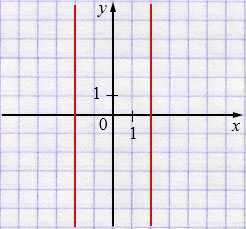
з) \(|y|=3\)
\(y=3\) или \( y=-3\)
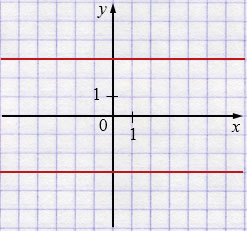
Пояснения:
\(x = a\) - прямая, параллельная оси \(y\) и проходящая через точку с координатами \((a; 0)\).
\(y = b\) - прямая, параллельная оси \(x\) и проходящая через точку с координатами \((0; b)\).
Если в уравнении стоит произведение двух множителей и оно равно нулю, \((f(x,y)\cdot g(x,y)=0)\), то график — объединение графиков \(f(x,y)=0\) и \(g(x,y)=0\).
Равенства \(|x|=a\ (a>0)\) и \(|y|=a\) задают пары параллельных прямых: \(|x|=a\) соответствует \(x=a\) и \(x=-a\) (две вертикальные), а \(|y|=a\) соответствует \(y=a\) и \(y=-a\) (две горизонтальные).
№675 учебника 2013-2022 (стр. 154):
\(ax^2 + bx + c = 0\)
\(a + b + c=0\)
\(b = - a-c \)
\(b= -(a+c)\)
\(ax^2 - (a+c)x + c = 0\)
\(D = b^2 - 4ac = \)
\(=(-(a + c))^2 - 4ac =\)
\(=a^2 + 2ac + c^2 - 4ac =\)
\(=a^2 -2ac +c^2 = (a-c)^2 \ge0\)
1 случай
Если \(a = c\), то \(D = 0\) и уравнение имеет один корень.
\(x = -\frac{-(a+c)}{2\cdot a} = \frac{с+c}{2\cdot с}=\frac{2c}{2c} = 1\).
2 случай
Если \(a \neq c\), то \(D > 0\) и уравнение имеет два корня.
\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)
1) Если \(a > c\), то
\(\sqrt D = \sqrt{(a - c)^2}= |a-c| = a-c\)
\(x_{1} = \frac{(a+c) + (a-c) }{2a} =\)
\(=\frac{a+c + a-c }{2a} = \frac{2a}{2a} = 1 \)
\(x_{2} = \frac{(a+c) - (a-c) }{2a} =\)
\(=\frac{a+c - a+c }{2a} = \frac{2c}{2a} = \frac{c}{a} \)
2) Если \(a < c\), то
\(\sqrt D = \sqrt{(a - c)^2}= |a-c| = c-a\)
\(x_{1} = \frac{(a+c) + (c-a) }{2a} =\)
\(=\frac{a+c +c-a }{2a} = \frac{2c}{2a} = \frac{c}{a} \)
\(x_{2} = \frac{(a+c) - (c-a) }{2a} =\)
\(=\frac{a+c - c+a }{2a} = \frac{2a}{2a} = 1 \)
Что и требовалось доказать.
а) \(2x^2 - 41x + 39 = 0\).
\(a = 2\), \(b = -41\), \(c = 39\)
\(2 - 41 + 39 = 0\), поэтому \(x_1 = 1\).
\( x_2 = \frac{c}{a} = \frac{39}{2} = 19,5\)
Ответ: \(x_1 = 1, \; x_2 = 19,5.\)
б) \(17x^2 + 243x - 260 = 0\)
\(a = 17\), \(b = 243\), \(c = -260\)
\(17 + 243 - 260 = 0\), поэтому \(x_1 = 1\).
\( x_2 = \frac{c}{a} = \frac{-260}{17} =-15\frac{5}{17}\)
| - | 2 | 6 | 0 | 1 | 7 | |||||||||
| 1 | 7 | 1 | 5 | |||||||||||
| - | 9 | 0 | ||||||||||||
| 8 | 5 | |||||||||||||
| - | 5 | 0 |
Ответ: \(x_1 = 1, \; x_2 = -15\frac{5}{17}.\)
Пояснения:
В задаче используется полезное: если сумма коэффициентов квадратного уравнения равна нулю, то корень \(x=1\). Это следует из того, что при подстановке \(x=1\) уравнение обращается в тождество.
Из доказательства данного свойства следует то, что один из корней равен единице, а другой равен отношению коэффициентов \(c\) и \(a\), то есть \(x_1 = 1\) и \( x_2 = \frac{c}{a}\).
Вернуться к содержанию учебника