Построение треугольника по двум сторонам и углу между ними

Задача:

Построить треугольник по двум сторонам и углу между ними с помощью циркуля и линейки (без масштабных делений).

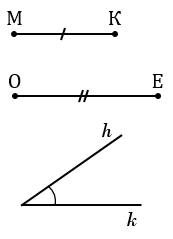
Дано: отрезки МК и ОЕ, 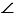hk.

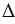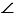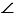Построить АВС такой, что АВ = МК, АС = ОЕ, ВАС =hk.

Решение:

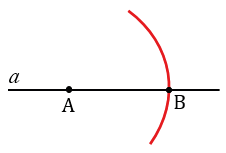
С помощью линейки проводим прямую 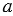и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой 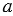ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой 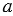обозначаем В.

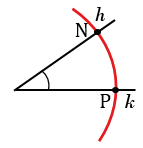
Далее строим угол ВАF равный углу hk. Для этого строим с помощью циркуля окружность радиуса МК с центром в вершине угла hk  (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла hk обозначаем N и Р.

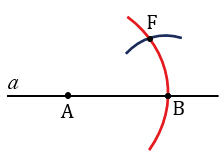
С помощью циркуля измеряем длину отрезка NP и строим окружность радиуса NP с центром в точке В (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения данной окружности с окружностью радиуса МК с центром в точке А обозначаем F.

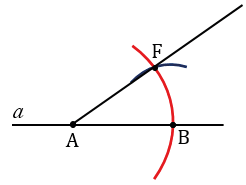
Далее, проводим луч АF с помощью линейки.

Затем, с помощью циркуля измеряем отрезок ОЕ и строим окружность радиуса ОЕ с центром в точку А (всю окружность строить необязательно, смотри, выделенное зеленым цветом). Точку пересечения данной окружности с лучом АF обозначаем С.

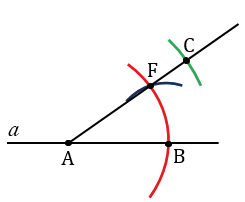
Теперь с помощью линейки соединяем точки В и С. Получаем треугольник АВС, в котором по построению АВ = МК, АС = ОЕ, 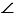ВАС =hk, следовательно, треугольник АВС - искомый.

При любых данных отрезках МК, ОЕ и данном неразвернутом угле hk искомый треугольник построить можно. Прямую 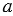и точку А на ней можно выбрать произвольно, значит, существует бесконечно много треугольников, удовлетворяющих условиям задачи, Все эти треугольники будут равны друг другу по первому признаку равенства треугольников (по двум сторонам и углу между ними), поэтому принято говорить, что данная задача имеет единственное решение.