Построение треугольника по трем его сторонам

Задача:

Построить треугольник по трем его сторонам.

Дано: отрезки МК, ОЕ, FG.

Построить 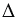АВС так, что АВ = МК, ВС = FG, АС = ОЕ.

Решение:

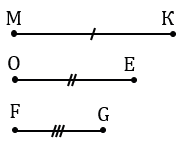
С помощью линейки проводим прямую 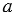и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой 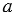ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой 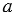обозначаем В.

Далее, с помощью циркуля измеряем отрезок ОЕ и строим окружность с центром в точке А радиуса ОЕ (всю окружность строить необязательно, смотри, выделенное синим цветом).

Далее, с помощью циркуля измеряем отрезок FG и строим окружность с центром в точке B радиуса FG (всю окружность строить необязательно, смотри, выделенное зеленым цветом).

Точку пересечения окружностей с центрами в точках А и В радиусами ОЕ и FG соответственно обозначаем С. Соединяем с помощью линейки точки А и В с точкой С. Получаем треугольник АВС, в котором по построению АВ = МК, ВС = FG, АС = ОЕ, следовательно, 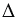АВС - искомый.

Данная задача не всегда имеет решение. Так как для каждого треугольника должно выполняться неравенство треугольника, которое говорит о том, что во всяком треугольнике сумма любых двух сторон больше третьей стороны. Если же какой-нибудь из данных отрезков будет больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.