Неравенство треугольника
Теорема
| Каждая сторона треугольника меньше суммы двух других сторон. |
Доказательство:
Дано:  АВС.
АВС.
Доказать: АВ ВС + АС.
ВС + АС.
Доказательство:
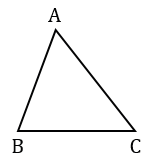
Сделаем дополнительное построение. Отложим на продолжении стороны ВС отрезок СD, равный стороне АС.
По построению СD = АС, следовательно,  АСD - равнобедренный с основанием АD, тогда
АСD - равнобедренный с основанием АD, тогда  1 =
1 = 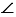 2 (углы при основании), при этом в
2 (углы при основании), при этом в  АВD
АВD 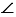 ВАD
ВАD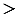
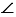 2, следовательно,
2, следовательно, 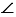 ВАD
ВАD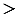
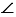 1.
1.
В треугольнике против большего угла лежит большая сторона, значит, АВ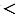 ВD. При этом ВD = ВС + СD, а учитывая то, что по построению СD = АС получим, ВD = ВС + АС, поэтому АВ
ВD. При этом ВD = ВС + СD, а учитывая то, что по построению СD = АС получим, ВD = ВС + АС, поэтому АВ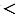 ВС + АС. Что и требовалось доказать.
ВС + АС. Что и требовалось доказать.
Следствие
Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ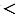 АС+СВ, АС АС+СВ, АС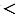 АВ+ВС, ВС АВ+ВС, ВС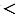 ВА+АС. ВА+АС. |
Каждое из неравенств АВ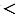 АС+СВ, АС
АС+СВ, АС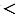 АВ+ВС, ВС
АВ+ВС, ВС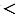 ВА+АС, называется неравенством треугольника.
ВА+АС, называется неравенством треугольника.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 248, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 304, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 305, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 760, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1176, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1232, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1262, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 315, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 320, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Упражнение 893, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 894, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1022, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1052, Макарычев, Миндюк, Нешков, Суворова, Учебник