Уголковый отражатель

Простейший уголковый отражатель представляет собой две зеркальные поверхности, расположенные под прямым углом друг к другу. Луч, падающий на одну из поверхностей, отражается от нее по закону отражения света: «угол падения светового луча  равен углу отражения луча». При этом угол между падающим лучом и поверхностью и угол между отраженным лучом и поверхностью также будут равны, так как они дополняют равные углы до прямого угла. В основе данной конструкции лежит свойство прямоугольного треугольника, которое говорит о том, что сумма двух острых  углов в нем равна 90⁰.

 Рассмотрим задачу:

Угол между зеркалами OA и OB равен 90⁰. Луч света, падающий на зеркало OA  под углом 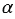, отражается от него, а затем отражается от зеркала ОВ. Доказать, что падающий и отражённый лучи параллельны.

Дано: 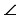АОВ = 90⁰, 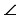AMC =

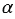
Доказать: MS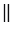NT

Доказательство:

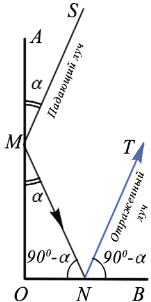
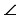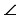AMS = OMN = 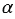(по закону отражения). 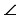MNO = 90⁰ - 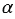(так как 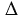MON - прямоугольный). 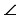MNO = 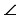TNB = 90⁰ - 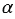(по закону отражения). По рисунку видим, что 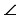SMN = 180⁰ - 2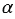, 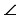MNT = 180⁰ - 2(90⁰ 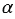- 2) = 2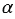, поэтому 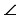SMN + 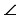MNT = 180⁰,  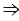 MS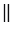NT (по признаку параллельности прямых, так как 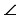SMN и 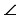MNT односторонние), что и требовалось доказать.

Уголковый отражатель "возвращает назад" падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей. Уголковый отражатель применяется в радиолокационных системах наблюдения, которые устанавливаются на самолетах-разведчиках, подводных лодках и позволяют обнаруживать различные объекты на земле и в воздухе. Также, с помощью уголкового отражателя нашим ученым удалось измерить расстояние от Земли до Луны.