Теорема о соотношениях между сторонами и углами треугольника
Теорема:
| В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона. |
Доказательство:
1) Дано:  АВС, АВ
АВС, АВ АС.
АС.
Доказать:  С
С
 В.
В.
Доказательство:
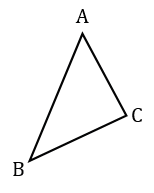
Отложим на стороне АВ отрезок АD, равный стороне АС.
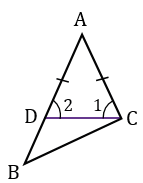
АD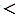 АВ, т.к. по построению АD = АС, а по условию АС
АВ, т.к. по построению АD = АС, а по условию АС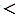 АВ, значит, точка D лежит между точками А и В. Следовательно,
АВ, значит, точка D лежит между точками А и В. Следовательно,  1 является частью
1 является частью  С, т.е.
С, т.е.  С
С
 1. Угол 2 внешний угол
1. Угол 2 внешний угол 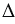 DBC, поэтому
DBC, поэтому  2
2
 В.
В. 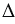 АDС - равнобедренный с основанием DC, т.к. по построению АD = АС, следовательно,
АDС - равнобедренный с основанием DC, т.к. по построению АD = АС, следовательно,  1 =
1 = 2 (углы при основании).
2 (углы при основании).
Итак,  С
С
 1,
1,  1 =
1 = 2, значит,
2, значит,  С
С
 2, при этом
2, при этом  2
2
 В, следовательно,
В, следовательно,  С
С
 В.
В.
2) Дано: 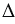 АВС,
АВС,  С
С
 В.
В.
Доказать: АВ АС.
АС.
Доказательство:

Предположим, что это не так. Тогда возможны два варианта:
- либо АВ = АС, тогда
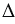 АВС - равнобедренный с основанием ВС, значит,
АВС - равнобедренный с основанием ВС, значит,  С =
С = В (как углы при основании), что противоречит условию:
В (как углы при основании), что противоречит условию:  С
С
 В.
В. - либо АВ
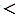 АС, тогда
АС, тогда  С
С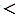
 В, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию:
В, т.к. против большей стороны лежит больший угол (смотри 1 часть доказательства), что противоречит условию:  С
С
 В.
В.
Значит, наше предположение неверно, следовательно, АВ АС. Что и требовалось доказать.
АС. Что и требовалось доказать.
Следствие 1
| В прямоугольном треугольнике гипотенуза больше катета. |
Доказательство:
Дано: 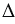 АВС, ВС - гипотенуза,
АВС, ВС - гипотенуза,  А - прямой.
А - прямой.
Доказать: ВС АС, ВС
АС, ВС  АВ.
АВ.
Доказательство:
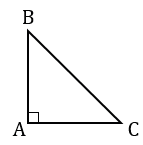
 АВС - прямоугольный,
АВС - прямоугольный,  А - прямой, следовательно, углы В и С острые, тогда
А - прямой, следовательно, углы В и С острые, тогда  А
А
 В и
В и  А
А
 С, значит, ВС
С, значит, ВС АС, ВС
АС, ВС АВ (в треугольнике против большего угла лежит большая сторона). Что и требовалось доказать.
АВ (в треугольнике против большего угла лежит большая сторона). Что и требовалось доказать.
Следствие 2
| Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника). |
Доказательство:
Дано:  АВС,
АВС,  В =
В = С.
С.
Доказать: АС = АВ.
Доказательство:
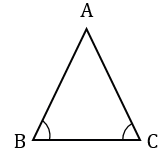
Предположим, что одна из сторон будет больше, т.е. АС АВ, тогда и угол лежащий против этой стороны будет больше, т.е.
АВ, тогда и угол лежащий против этой стороны будет больше, т.е.  В
В
 С (в треугольнике против большей стороны лежит больший угол), а это противоречит условию:
С (в треугольнике против большей стороны лежит больший угол), а это противоречит условию:  В =
В = С, следовательно, наше предположение неверно, значит АС = АВ.
С, следовательно, наше предположение неверно, значит АС = АВ.
Итак, в 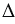 АВС равны две стороны (АС = АВ), следовательно, данный треугольник - равнобедренный. Что и требовалось доказать.
АВС равны две стороны (АС = АВ), следовательно, данный треугольник - равнобедренный. Что и требовалось доказать.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 237, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 239, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 240, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 256, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 340, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 524, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 821, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 848, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1025, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 408, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник