Сравнение десятичных дробей / Десятичные дроби / Справочник по математике 5-9 класс

Сравнение десятичных дробей

Одно и то же натуральное число может быть представлено в виде обыкновенной дроби разными способами, например, 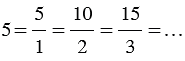. Для десятичных дробей также справедливо такое свойство, так, например, десятичные дроби 0,5, 0,50 и 0,500 обозначают одно и то же число.

Если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.

Пример:

1) 1,3 = 1,30 = 1,300 = ...;

2) 3,67 = 3,670 = 3,6700 = ... .

Если в десятичной дроби последние цифры - нули, то, отбросив их, получим дробь, равную данной.

Пример:

1) 3,40 = 3,4; 2) 0,50600 = 0,506; 3) 5,870000 = 5,87.

Любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.

Пример:

1) 8 = 8,0 = 8,00 = 8,000 = ...;

2) 125 = 125,0 = 125,00 = 125,000 = ... .

Из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше.

Пример:

1) 3,5 2,96; 2) 0,567 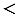4,2.

Из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение).

Пример:

1) 15,2 15,1; 2) 2,65 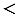2,68; 3) 345,548 345,547.

Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно (смотри правило выше).

Пример:

Сравнить десятичные дроби 45,6 и 45,498.

Решение:

У дроби 45,6 одна цифра после запятой, а у дроби 45,498 три цифры после запятой, для того, чтобы сравнить данные дроби, приписываем к дроби 45,6 справа два нуля, получим новую дробь 45,600. Теперь поразрядно сравниваем дроби 45,600 и 45,498, получим 45,600 45,498, т.к. 6 4, значит, и 45,6 45,498.

Сравнение десятичных дробей

Советуем посмотреть:

Правило встречается в следующих упражнениях: