Номер 456 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 115

1) А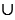В = А.

2) А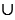В = N(кроме 1).

3) А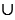В = {2, 1, 3, 5 ....2k+1}, где k - натуральное число.

Пояснения:

Словом "множество" в математическом языке обозначают любую совокупность объектов или предметов, объединенных каким-либо общим признаком. Объекты, которые составляют данное множество, называют элементами этого множества. Объединением множества А и В называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств: или множеству А, или множеству В. Объединение множеств А и В обозначают так: А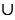В.

1) Нам даны: А - множество равнобедренных треугольников, В - множество равносторонних треугольников. Равнобедренный треугольник - это треугольник, у которого две стороны равны. Равносторонний треугольник - это треугольник, у которого все стороны равны. Из чего мы можем сделать вывод, что равносторонний треугольник, также является равнобедренным, значит, все элементы множества В принадлежат также множеству А, поэтому объединением данных множеств будет множество А, то есть запишем:

А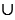В = А.

2) Нам даны: А - множество простых чисел, В - множество составных чисел. Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. Натуральное число называют составным, если оно имеет больше двух натуральных делителей. При этом  1 не относят ни к составным числам, ни к простым, так как оно имеет только один делитель. То есть объединением данных множеств будет множество натуральных за исключением 1, получаем:

А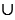В = N(кроме 1).

3) Нам даны: А - множество простых чисел, В - множество нечётных чисел. Так как простые числа имеет только 2 множителя (1 и само это число), то все простые числа, кроме 2, являются нечетными, а значит, входят в множество В, то есть объединением данных множеств будет множество, состоящее из 2 и всех нечетных чисел, получаем:

А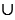В = {2, 1, 3, 5 ....2k+1}, где k - натуральное число.