Упражнение 61 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 18
Вернуться к содержанию учебника
Вопрос
(Для работы в парах.) Докажите, что всякое простое число, начиная с 5, либо увеличенное, либо уменьшенное на 1, делится на 6.
1) Проверьте утверждение на примерах. Одному учащемуся рекомендуем взять простые числа из третьего десятка, другому - из седьмого десятка.
2) Обсудите друг с другом, из чего следует справедливость указанного свойства.
3) Проведите доказательство.
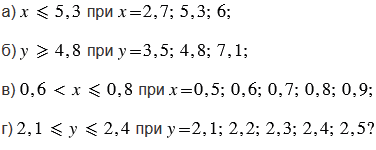
Подсказка
Вспомните:
- Какие числа называют простыми.
- Четные и нечетные числа.
Ответ
23 и 29 - простые числа из третьего десятка.
23 - 1 = 22 - не делится на 6,
23 + 1 = 24 - делится на 6.
29 - 1 = 28 - не делится на 6.
29 + 1 = 30 - делится на 6.
61, 67 - простые числа из шестого десятка.
61 - 1 = 60 - делится на 6.
61 + 1 = 62 - не делится на 6.
67 - 1 = 66 - делится на 6.
67 + 1 = 68 - не делится на 6.
Доказательство:
Пусть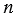 
- простое число равное 5 или большее 5.
Все простые числа, кроме числа 2, являются нечетными числами. Если из нечетного числа вычесть единицу или к нечетному числу прибавить единицу, то получится четное число, которое делится на 2, то есть числа (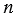 - 1) и ( 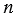+ 1) делятся на 2.
Числа (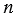 - 1), 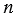, ( 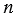+ 1) - три последовательных числа. Среди трех последовательных чисел одно число всегда делится на 3. Число на 3 не может делится, так как оно простое, значит, на 3 будет делится либо число ( 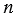- 1), либо число ( 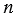+ 1). А любое число, которое делится на 2 и на 3, делится и на 6. Что и требовалось доказать.
Вернуться к содержанию учебника