Задание 2.124 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Выберите год учебника
Вопрос
№2.124 учебника 2023-2024 (стр. 58):
Запишите в виде смешанного числа:
а) 31 : 9;
б) 81 : 9;
в) 402 : 15;
г) 1429 : 14.
№2.124 учебника 2021-2022 (стр. 52):
Найдите НОД (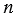
; 
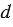) если:
а) 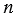= 3 • 5 • 7 • 7 • 11, 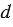= 5 • 5 • 7 • 11;
б) 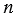= 756, 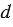= 720.
Подсказка
№2.124 учебника 2023-2024 (стр. 58):
Вспомните:
- Смешанные числа.
- Обыкновенные дроби (неправильные дроби).
- Деление и дроби.
- Сокращение дробей.
- Наибольший общий делитель.
№2.124 учебника 2021-2022 (стр. 52):
Вспомните:
- Как найти наибольший общий делитель (НОД).
- Разложение на простые множители.
- Какие числа называют простыми.
- Умножение чисел.
Ответ
№2.124 учебника 2023-2024 (стр. 58):
| - | 1 | 4 | 2 | 9 | 1 | 4 | |||||
| 1 | 4 | 1 | 0 | 2 | |||||||
| - | 2 | 9 | |||||||||
| 2 | 8 | ||||||||||
| - | 1 | - | о | с | т | . |
Пояснения:
Частное всегда можно записать в виде обыкновенной дроби, у которой делимое - числитель, делитель - знаменатель. В нашем случае получатся неправильные дроби, то есть дроби у которых числитель больше знаменателя, которые нужно преобразовать в смешанные числа. При этом, обратите внимание, если получается сократимая дробь, мы ее сначала сокращаем (делим числитель и знаменатель на их наибольший общий делитель).
Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
№2.124 учебника 2021-2022 (стр. 52):
а)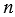 
= 3 • 5 • 7 • 7 • 11
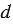= 5 • 5 • 7 • 11
НОД(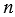; 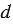) = 5 • 7 • 11 = 35 • 11 = 385
| × | 3 | 5 | |
| 1 | 1 | ||
| + | 3 | 5 | |
| 3 | 5 | ||
| 3 | 8 | 5 |
Ответ: НОД(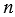; 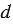) = 385.
б) 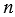= 756 = 2 • 2 • 3 • 3 • 3 • 7
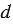= 720 = 2 • 2 • 2 • 2 • 3 • 3 • 5
НОД(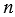; 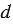) = 2 • 2 • 3 • 3 = 4 • 9 = 36
Ответ: НОД(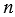; 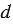) = 36.
Пояснения:
Наибольшим общим делителем (НОД) нескольких чисел называют наибольшее натуральное число, на которое делятся эти числа без остатка.
Если из двух чисел большее число делится на меньшее, то наибольшим общим делителем этих двух чисел будет меньшее число.чисел.
Чтобы найти наибольший общий делитель нескольких чисел, надо:
1) разложить числа на простые множители;
2) выбрать общие множители в каждом разложении;
3) найти произведение общих множителей.
Представление числа в виде произведения его простых делителей называют разложением числа на простые множители.
Признаки делимости помогают при разложении числа на простые множители. При этом запись удобно вести с помощью вертикальной черты.
Число делится на 5, если это число оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Число делится на 2, если это число оканчивается четной цифрой (0; 2; 4; 6 или 8).
Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
При выполнении умножения, опираясь на переместительное и сочетательное свойство умножения, группируем множители так как нам удобно (чтобы вычисления были проще).
Вернуться к содержанию учебника