Упражнение 364 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 115
Вернуться к содержанию учебника
Вопрос
Постройте график уравнения:
а) \(2y - 0{,}5x^2 = 0;\)
б) \(x^2 - 3y = 6;\)
в) \(4x^2 = 8 - y;\)
г) \(-5x^2 + 2y = 3.\)
Подсказка
Вспомните:
- Уравнения с двумя переменными, их свойства.
- График квадратичной функции.
- Координаты точки на координатной плоскости.
- Степень с натуральным показателем.
- Деление рациональных чисел.
- Деление и дроби.
- Умножение десятичных дробей.
- Умножение рациональных чисел.
- Умножение обыкновенных дробей.
- Десятичная запись дробных чисел.
Ответ
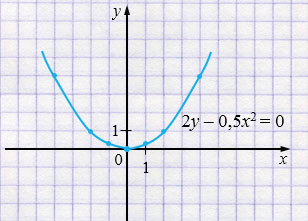
а) \(2y - 0,5x^2 = 0\)
\( 2y = 0{,}5x^2 \) \(/ : 2\)
\(y = 0{,}25x^2\) - парабола, ветви которой направлены вверх.
| \(x\) | \(-4\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(4\) |
| \(y\) | \(4\) | \(1\) | \(0,25\) | \(0\) | \(0,25\) | \(1\) | \(4\) |
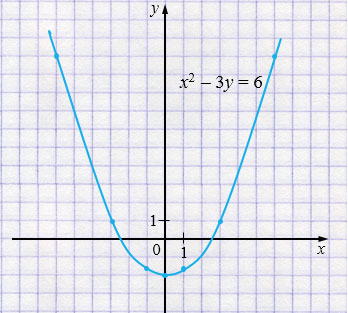
б) \(x^2 - 3y = 6\)
\( -3y = 6 - x^2 \) \(/ : (-3)\)
\(y = \frac{1}{3}x^2 - 2\) - парабола, ветви которой направлены вверх.
| \(x\) | \(-6\) | \(-3\) | \(-1\) | \(0\) | \(1\) | \(3\) | \(6\) |
| \(y\) | \(10\) | \(1\) | \(1\frac23\) | \(-2\) | \(1\frac23\) | \(1\) | \(10\) |
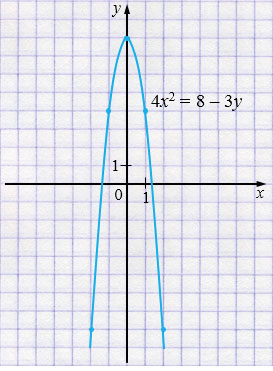
в) \(4x^2 = 8 - y\)
\( y = -4x^2 + 8 \) - парабола, ветви которой направлены вниз.
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(y\) | \(-8\) | \(4\) | \(8\) | \(4\) | \(-8\) |
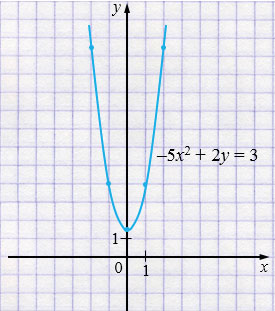
г) \(-5x^2 + 2y = 3\)
\( 2y = 5x^2 + 3 \) \(/ : 2\)
\(y = \frac{5}{2}x^2 + \frac{3}{2}\)
\(y = 2,5x^2 + 1,5\) - парабола, ветви которой направлены вверх.
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(y\) | \(11,5\) | \(4\) | \(1,5\) | \(4\) | \(11,5\) |
Пояснения:
Каждый график является параболой, так как уравнения приводятся к виду \(y = ax^2 + b\).
Знак коэффициента при \(x^2\) определяет направление ветвей:
- \(a>0\): ветви вверх;
- \(a<0\): ветви вниз.
Графики строим по точкам, составляя таблицы
Вернуться к содержанию учебника