Упражнение 365 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 115
Вернуться к содержанию учебника
Вопрос
Постройте график уравнения:
а) \(3xy = 12;\)
б) \(\frac12 xy = 6;\)
в) \(2xy = -8;\)
г) \(\frac12 xy = -6.\)
Подсказка
Вспомните:
- Уравнения с двумя переменными, их свойства.
- График функции \(y = \frac kx\).
- Координаты точки на координатной плоскости.
- Деление рациональных чисел.
- Деление и дроби.
- Умножение обыкновенных дробей.
- Умножение рациональных чисел.
- Десятичная запись дробных чисел.
- Деление десятичных дробей.
Ответ
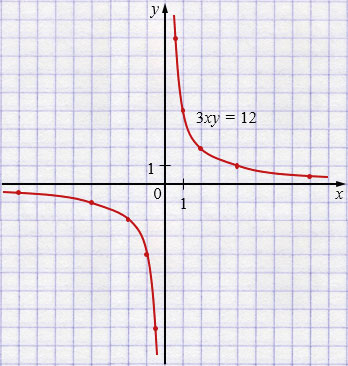
а) \(3xy = 12\)
\(y = \frac{12}{3x}\)
\(y = \frac{4}{x}\) - гипербола в I и III четвертях.
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(-0,5\) |
| \(y\) | \(-0,5\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) |
| \(x\) | \(0,5\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y\) | \(8\) | \(4\) | \(2\) | \(1\) | \(0,5\) |
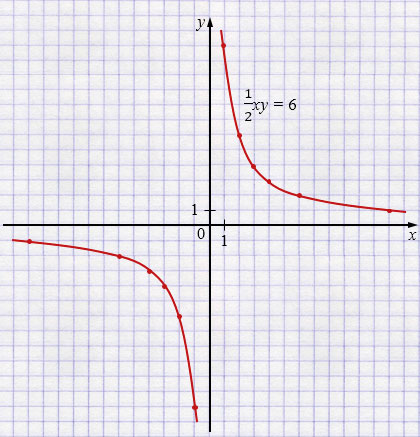
б) \(\frac12 xy = 6\) \(/\times2\)
\(xy = 12\)
\(y = \frac{12}{x}\) - гипербола в I и III четвертях.
| \(x\) | \(-12\) | \(-6\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) |
| \(y\) | \(-1\) | \(-3\) | \(-3\) | \(-4\) | \(-6\) | \(-12\) |
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(6\) | \(12\) |
| \(y\) | \(12\) | \(6\) | \(4\) | \(3\) | \(2\) | \(1\) |
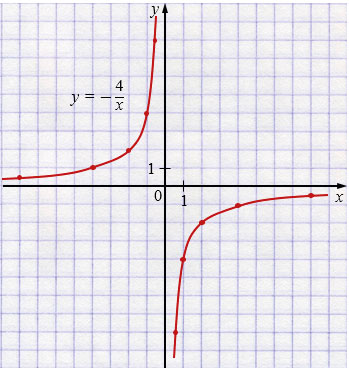
в) \(2xy = -8\)
\(y = -\frac{8}{2x}\)
\(y = -\frac{4}{x}\) - гипербола во II и IV четвертях.
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(-0,5\) |
| \(y\) | \(0,5\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(x\) | \(0,5\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(-0,5\) |
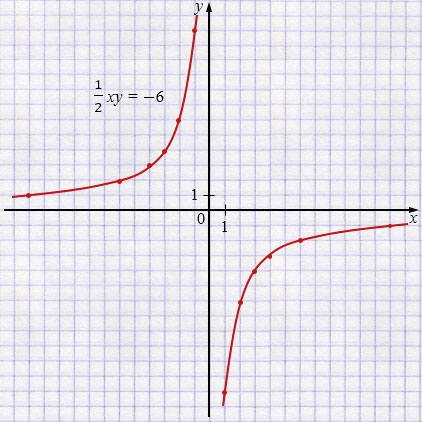
г) \(\frac12 xy = -6\) \(/\times2\)
\( xy = -12 \)
\(y = -\frac{12}{x}\) - гипербола во II и IV четвертях.
Пояснения:
Графики всех уравнений имеют вид гиперболы, так как приводятся к виду \(y = \frac{k}{x}\).
Если \(k>0\), ветви гиперболы расположены в I и III четвертях; если \(k<0\) — во II и IV четвертях.
Графики строим по точкам, составляя таблицы
Вернуться к содержанию учебника