Упражнение 359 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 114

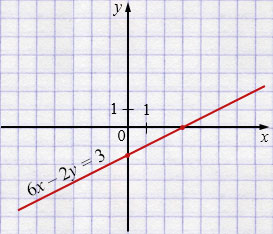
а) \(x - 2y = 3\) - прямая.

С осью \(x\): \(y = 0\).

\(x - 2\cdot 0 = 3\)

\(x = 3\).

\((3; 0)\) - точка пересечения с осью \(x\).

С осью \(y\): \(x = 0\).

\(0 - 2y = 3 \)

\(-2y = 3\)

\(y = -\dfrac{3}{2}\)

\(y = -1,5\)

\((0; -1,5)\) - точка пересечения с осью \(y\).

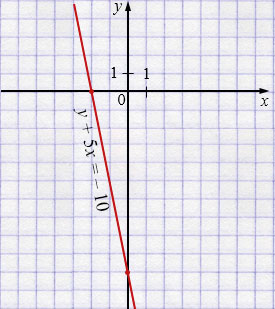
б) \(y + 5x = -10\) - прямая.

С осью \(x\): \(y = 0\).

\(0 + 5x = -10 \)

\(5x = -10\)

\(x = -\frac{10}{5}\)

\(x = -2\).

\((-2;0)\) - точка пересечения с осью \(x\).

С осью \(y\): \(x = 0\).

\(y + 0 = -10 \)

\(y = -10\).

\((0; -10)\) - точка пересечения с осью \(y\).

в) \(4x - 0{,}5y = 2\) - прямая.

С осью \(x\): \(y = 0\).

\(4x - 0,5\cdot 0 = 2\)

\(4x = 2\)

\(x = \dfrac24\)

\(x = 0,5\)

\((0,5;0)\) - точка пересечения с осью \(x\).

С осью \(y\): \(x = 0\).

\(4\cdot 0 - 0,5y = 2\)

\(-0{,}5y = 2\)   \(/\times (-2)\)

\(y = -4\).

\((0;-4)\) - точка пересечения с осью \(y\).

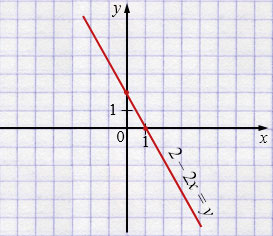
г) \(2 - 2x = y\)

\(y = 2 - 2x\) - прямая.

С осью \(x\): \(y = 0\).

\(0 = 2 - 2x\)

\(2x = 2 \)

\(x = 1\).

\((1; 0)\) - точка пересечения с осью \(x\).

С осью \(y\): \(x = 0\).

\(y = 2 - 2\cdot 0 = 2\).

\((0; 2)\) - точка пересечения с осью \(y\).

Пояснения:

Чтобы найти точку пересечения графика с осью \(x\), нужно подставить \(y=0\) в уравнение. Это даёт точку вида \((x_0,0)\).

Чтобы найти точку пересечения с осью \(y\), подставляем \(x=0\). Получаем точку вида \((0,y_0)\).

Каждое из данных уравнений линейное, значит его график — прямая. По двум найденным точкам строим график.