Упражнение 361 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 115

а) \(\begin{cases} 2x + 5y = 8,\\ y - 3x = 5 \end{cases}\)

1) \(2x + 5y = 8\) - прямая.

\(5y = -2x + 8\)   \(/ : 5\)

\(y = -\frac25x + \frac85\)

\(y = -0,4x + 1,6\)

\(k = -0,4 > 0, \Rightarrow\) прямая убывающая.

\(m = 1,6 > 0, \Rightarrow\) прямая пересекает ось \(y\) выше оси \(х\).

2) \(y - 3x = 5\) - прямая.

\(y = 3x + 5\)

\(k = 3 > 0, \Rightarrow\) прямая возрастающая.

\(m = 5 > 0, \Rightarrow\) прямая пересекает ось \(y\) выше оси \(х\).

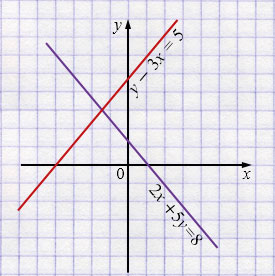
Ответ: точка пересечения лежит во II четверти.

б) \(\begin{cases} 5x - 2y = 2,\\ x + 0{,}5y = 4 \end{cases}\)

1) \(5x - 2y = 2\)

\(-2y = -5x + 2\)   \(/ : (-2)\)

\(y = \frac52x - 1\)

\(y = 2,5x - 1\)

\(k = 2,5 > 0, \Rightarrow\) прямая возрастающая.

\(m = -1 < 0, \Rightarrow\) прямая пересекает ось \(y\) ниже оси \(х\).

2) \(x + 0{,}5y = 4\)

\(0,5y = -x + 4\)   \(/\times2\)

\(y = -2x + 8\)

\(k = -2 < 0, \Rightarrow\) прямая убывающая.

\(m = 8 > 0, \Rightarrow\) прямая пересекает ось \(y\) выше оси \(х\).

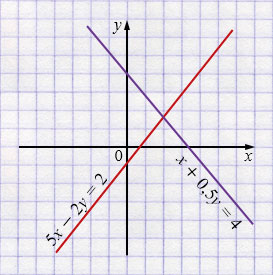
Ответ: точка пересечения лежит в I четверти.

Пояснения:

Чтобы схематически изобразить графики линейных уравнений вида \(ax + by =c\) и определить, в каких координатных четвертях лежат точки пересечения графиков, нужно, используя свойства уравнений, привести уравнения к виду

\(у = kx + m\).

Коэффициент \(k\) показывает возрастающая при \(k > 0\) или убывающая при \(k < 0\) будет прямая. Коэффициент \(m\) отвечает за точку пересечения с осью \(y\), если \(m > 0\), то прямая пересекает ось \(y\) выше оси \(x\), если \(m < 0\), то прямая пересекает ось \(y\) ниже оси \(x\).