Упражнение 366 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 115
Вернуться к содержанию учебника
Вопрос
График уравнения \(xy = k\) проходит через точку \((-2;\,4)\). Найдите число \(k\) и постройте этот график.
Подсказка
Вспомните:
- Уравнения с двумя переменными, их свойства.
- График функции \(y = \frac kx\).
- Координаты точки на координатной плоскости.
- Деление рациональных чисел.
- Деление и дроби.
- Умножение рациональных чисел.
Ответ
\[ x y = k \]
\((-2; 4)\)
\[ (-2)\cdot 4 = k\]
\[ k = -8 \]
\( xy = -8 \)
\(y = -\frac{8}{x}\) - гипербола, ветви во II и IV четвертях.
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) |
| \(y\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(x\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) |
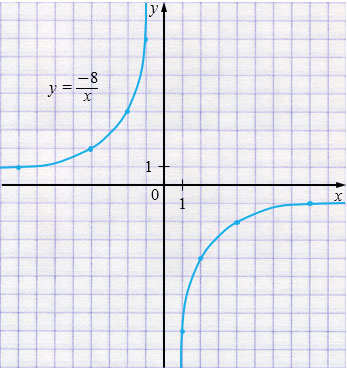
Пояснения:
Если гипербола \(xy=k\) проходит через точку \((x_0, y_0)\), то \(k = x_0 y_0\).
Чтобы построить график приводим уравнение к виду \(y = \frac{k}{x}\).
Если \(k>0\), ветви гиперболы расположены в I и III четвертях; если \(k<0\) — во II и IV четвертях.
Графики строим по точкам, составляя таблицы.
Вернуться к содержанию учебника