Упражнение 303 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 103

а) \( p^{3} - p^{2} = 8p - 12\)

\( p^{3} - p^{2} - 8p + 12 = 0 \)

\(\pm1;\, \pm2; \pm3; \pm4; \pm6; \pm12\) - делители числа 12.

Если \(p = 1\), то

\( 1^{3} - 1^{2} - 8\cdot1 + 12 = 0\)

\(1 - 1 - 8 + 12 = 0\)

\(4 = 0\) - неверно.

Если \(p = -1\), то

\( (-1)^{3} - (-1)^{2} - 8\cdot(-1) + 12 = 0\)

\(-1 - 1 + 8 + 12 = 0\)

\(18 = 0\) - неверно.

Если \(p = 2\), то

\( 2^{3} - 2^{2} - 8\cdot2 + 12 =0\)

\(8 - 4 - 16 + 12 = 0\)

\(0 = 0\) - верно.

\(p = 2\) — корень уравнения.

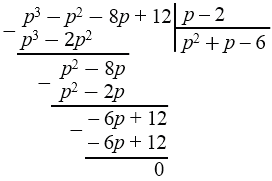
\( p^{3} - p^{2} - 8p + 12 = (p - 2)(p^{2} + p - 6)\)

\( (p - 2)(p^{2} + p - 6) = 0\)

\( p^{2} + p - 6 = 0\)

\(D = 1^2 - 4\cdot1\cdot(-6) =\)

\(=1 + 24 = 25 > 0\) - 2 корня.

\(\sqrt {25} = 5\).

\(p_{1} = \frac{-1 + 5}{2\cdot1} = \frac42=2\).

\(p_{2} = \frac{-1 - 5}{2\cdot1} = \frac{-6}{2}=-3\).

Ответ: \(2,\; -3.\)

б) \( p^{3} - 3p = p^{2} + 1\)

Переносим всё в левую часть:

\(p^{3} - p^{2} - 3p - 1 =0\)

\(\pm1\) - делители числа \(1\).

Если \(p=1\), то

\(1^{3} - 1^{2} - 3\cdot1 - 1 =0\)

\(1 - 1 - 3 - 1 = 0\)

\(-4 = 0\) - неверно.

Если \(p = -1\), то

\( (-1)^{3} - (-1)^{2} - 3(-1) - 1 =0\)

\(-1 - 1 + 3 - 1 = 0\)

\(0 = 0\) - верно.

\(p = -1\) — корень уравнения.

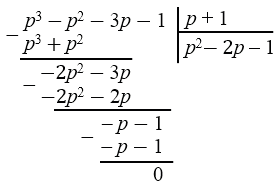
\( p^{3} - p^{2} - 3p - 1 = (p + 1)(p^{2} - 2p - 1)\)

\((p + 1)(p^{2} - 2p - 1)=0\)

\((p^{2} - 2p - 1)=0\)

\( D = (-2)^{2} - 4\cdot1\cdot(-1) =\)

\(=4 + 4 = 8> 0\) - 2 корня.

\(\sqrt 8 = \sqrt{4\cdot2} = 2\sqrt2\).

\( p_{1,2} = \frac{2 \pm 2\sqrt{2}}{2} = 1 \pm \sqrt{2}. \)

Ответ: \(-1;\; 1 + \sqrt{2};\; 1 - \sqrt{2}.\)

Пояснения:

Чтобы найти значения \(p\), при которых два выражения равны, нужно приравнять их и получить уравнение. Затем все слагаемые из правой части уравнения переносим в левую со сменой знака и в левой части получаем многочлен третьей степени.

Если многочлен имеет целый корень, то он является делителем свободного члена (последнего числового коэффициента). Поэтому для уравнений с целыми коэффициентами удобно проверять несколько простых значений \(x\) (например, \(\pm1, \pm2, \pm3,\dots\)). Найденное значение, при котором многочлен обращается в ноль, даёт линейный множитель \((x - x_0)\).

После нахождения корня \(x_0\) мы делим многочлен на \((x - x_0)\) (столбиком) и получаем многочлен меньшей степени. Процесс можно повторять, пока степень не станет 2, а затем решить квадратное уравнение стандартными способами (формула дискриминанта, разложение на множители).

Квадратное уравнение \(ax^{2} + bx + c = 0\) решается через дискриминант \(D = b^2 - 4ac\). Если \(D > 0\), то уравнение имеет 2 корня:

\[ x_{1,2} = \dfrac{-b \pm \sqrt{D}}{2a}. \]