Упражнение 308 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 104

а) \(x^{3} + 11x - 108 = 0\)

\(\pm1; \pm2; \pm3; \pm4; \pm6; \dots\) - делители числа 108.

Если \(x= 1\), то

\(1^{3} + 11\cdot1 - 108 = 0\)

\(1 + 11 - 108 = 0\)

\(-96 = 0\) - неверно.

Если \(x= 2\), то

\(2^{3} + 11\cdot2 - 108 = 0\)

\(8 + 22 - 108 = 0\)

\(-78 = 0\) - неверно.

Если \(x= 3\), то

\(3^{3} + 11\cdot3 - 108 = 0\)

\(27 + 33 - 108 = 0\)

\(-48 = 0\) - неверно.

Если \(x = 4\), то

\( 4^{3} + 11\cdot 4 - 108 = 0\)

\(64 + 44 - 108 = 0\)

\(0 = 0\) - верно.

\(x = 4\) — корень уравнения.

\(x^{3} = -11x + 108 \)

\(y = x^3\) - возрастающая функция.

\(y = -11x + 108 \) - убывающая функция.

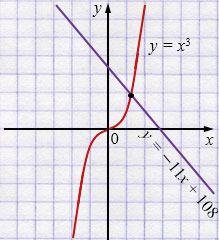
\(x = 4\) - единственный корень.

Ответ: \(x = 4\).

б) \(x^{5} + 6x + 44 = 0\)

\(\pm1; \pm2; \pm4; \dots\) - делители числа 44.

Если \(x = -1\), то

\((-1)^{5} + 6\cdot(-1) + 44 = 0\)

\(-1 - 6 + 44 = 0\)

\(37 = 0\) - неверно.

Если \(x = -2\), то

\( (-2)^{5} + 6(-2) + 44 =0\)

\(-32 - 12 + 44 = 0\)

\(0 = 0\) - верно.

\(x = -2\) — корень уравнения.

\(x^{5} = -6x - 44\)

\(y = x^5\) - возрастающая функция.

\(y = -6x - 44\) - убывающая функция.

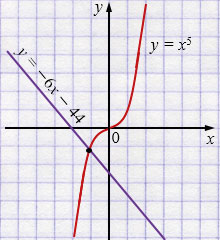
\(x = -2\) — единственный корень.

Ответ: \(x = -2\).

Пояснения:

Для многочленов с целыми коэффициентами часто ищут целые корни среди делителей свободного члена.

В каждом случае определили целый корень из делителей свободного члена, а затем каждое уравнение представили в виде равенства двух функций, одна из которых является возрастающей, а другая - убывающей. Возрастающая и убывающая функции могут пресекаться только в одной точке, а это говорит о том, что рассматриваемые уравнения имеют единственный корень, который мы нашли среди делителей свободного члена.