Упражнение 1116 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1116 учебника 2023-2025 (стр. 250):
При каких значениях \(x\) функция \(y = f(x)\) обращается в нуль, принимает положительные и отрицательные значения, если:
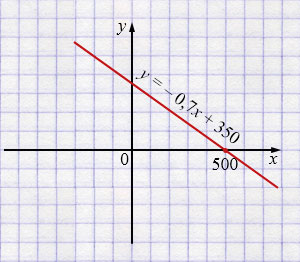
а) \(f(x) = -0{,}7x + 350;\)
б) \(f(x) = 30x + 10.\)
Начертите схематически график функции и проиллюстрируйте на нём установленные свойства.
№1116 учебника 2013-2022 (стр. 255):
Найдите все целые значения функции \[ y=\sqrt{\,12+2\sqrt{35+2x-x^{2}}\,}-\sqrt{\,12-2\sqrt{35+2x-x^{2}}\,}, \] которые она принимает при целых \(x\).
Подсказка
№1116 учебника 2023-2025 (стр. 250):
Вспомните:
- Линейную функцию, ее график и свойства.
- Координаты точки.
- Числовые промежутки.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Умножение рациональных чисел.
- Деление рациональных чисел.
№1116 учебника 2013-2022 (стр. 255):
Вспомните:
- Целые числа.
- Арифметический квадратный корень.
- Свойства арифметического квадратного корня.
- Модуль числа.
- Квадрат разности двух выражений.
- Разность квадратов двух выражений.
- Решение неравенств с одной переменной.
- Раскрытие скобок.
- Сложение рациональных чисел.
Ответ
№1116 учебника 2023-2025 (стр. 250):
а) \(y = f(x)\)
\(f(x) = -0{,}7x + 350\)
\( -0{,}7x + 350 = 0 \)
\(-0{,}7x = -350 \)
\(x = \frac{-350}{-0,7}\)
\(x = \frac{3500}{7}\)
\(x = 500 \)
\(k = -0{,}7 < 0\) - функция убывает, поэтому
— \(y > 0\) при \(x < 500\);
— \(y = 0\) при \(x = 500\);
— \(y < 0\) при \(x > 500\).
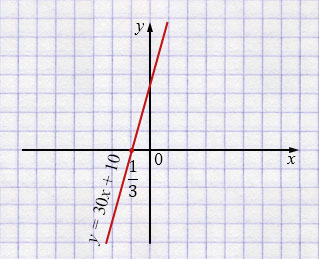
б) \(y = f(x)\)
\(f(x) = 30x + 10\)
\(30x + 10 = 0 \)
\(30x = -10 \)
\(x =-\frac{10}{30}\)
\(x = -\frac{1}{3} \)
\(k = 30 > 0\) - функция возрастает, поэтому:
— \(y < 0\) при \(x < -\frac{1}{3}\);
— \(y = 0\) при \(x = -\frac{1}{3}\);
— \(y > 0\) при \(x > -\frac{1}{3}\).
Пояснения:
Функцию, которую можно задать формулой вида \(y = kx + b\), \(k\) и \(b\) - некоторые числа, \(x\) - независимая переменная, называют линейной. Графиком линейной функции является прямая. График строят по двум точкам, так как прямая однозначно задается двумя точками.
1. Функция определена при любых значениях переменной \(x\), т.е.
\(D(y) = R\).
2. Значение функции может быть любое число, т.е. \(E(y) = R\).
3. Функция обращается в нуль при \(x = -\frac{b}{k}\).
Это свойство вытекает из решения уравнения \(kx + b = 0\), откуда получаем \(kx = -b\), тогда \(x = -\frac{b}{k}\).
4. При \(k > 0\) функция принимает отрицательные значения на промежутке \((-\infty; -\frac{b}{k})\) и положительные значения на промежутке \((-\frac{b}{k}; +\infty)\).
При \(k < 0\) функция принимает отрицательные значения на промежутке \((-\frac{b}{k}; +\infty)\) и положительные значения на промежутке \((-\infty; -\frac{b}{k})\).
5. При \(k>0\) функция \(y = kx + b\) является возрастающей, а при \(k < 0\) - убывающей.
№1116 учебника 2013-2022 (стр. 255):
\( y=\sqrt{12+2\sqrt{35+2x-x^{2}}}-\sqrt{12-2\sqrt{35+2x-x^{2}}}\)
\( y^2=\left(\sqrt{12+2\sqrt{35+2x-x^{2}}}-\sqrt{12-2\sqrt{35+2x-x^{2}}}\right)^2\)
\( y^2=\left(\sqrt{12+2\sqrt{35+2x-x^{2}}}\right)^2-2\sqrt{12+2\sqrt{35+2x-x^{2}}}\cdot\sqrt{12-2\sqrt{35+2x-x^{2}}}+\left(\sqrt{12-2\sqrt{35+2x-x^{2}}}\right)^2\)
\( y^2=12+\cancel{2\sqrt{35+2x-x^{2}}}-2\sqrt{(12+2\sqrt{35+2x-x^{2}})\cdot(12-2\sqrt{35+2x-x^{2}})}+2-\cancel{2\sqrt{35+2x-x^{2}}}\)
\( y^2=24 - 2\sqrt{(12^2-\left(2\sqrt{35+2x-x^{2}}\right)^2}\)
\( y^2=24 - 2\sqrt{144-4\cdot(35+2x-x^{2})}\)
\( y^2=24 - 2\sqrt{144-140-8x+4x^{2}}\)
\( y^2=24 - 2\sqrt{4-8x+4x^{2}}\)
\( y^2=24 - 2\sqrt{4(1-2x+x^{2})}\)
\( y^2=24 - 2\cdot2\sqrt{(x^{2}-1)^2}\)
\( y^2=24 - 4|x-1|\)
\( y^2=4(6 - |x-1|)\)
\(y \ge 0\)
\( y=\sqrt{4(6 - |x-1|)}\)
\( y=2\sqrt{6 - |x-1|}\)
1) Если \(x - 1 \ge 0\), то есть \(x\ge1\), то
\( y=2\sqrt{6 - (x-1)} =\)
\(=2\sqrt{6 - x +1}=2\sqrt{7-x}\)
Если \(x = 3\), то
\(y=2\sqrt{7-3} = 2\sqrt4 = 2\cdot2=4\) - целое число.
Если \(x = 6\), то
\(y=2\sqrt{7-6} = 2\sqrt1 = 2\cdot1=2\) - целое число.
Если \(x = 7\), то
\(y=2\sqrt{7-7} = 2\sqrt0 =0\) - целое число.
2) Если \(x - 1 < 0\), то есть \(x<1\), то
\( y=2\sqrt{6 + (x-1)} =\)
\(=2\sqrt{6 + x -1}=2\sqrt{5+x}\)
Если \(x = -1\), то
\(y=2\sqrt{5+(-1)} = 2\sqrt4=2\cdot2 = 4\) - целое число.
Если \(x = -4\), то
\(y=2\sqrt{5+(-4)} = 2\sqrt1=2\cdot1 = 2\) - целое число.
Если \(x = -5\), то
\(y=2\sqrt{5+(-5)} = 2\sqrt0=0\) - целое число.
Ответ: \(0; 2; 4\).
Пояснения:
Левую и правую части функции возводим в квадрат, учитывая то, что \(y\ge0\), так как
\(\sqrt{12+2\sqrt{35+2x-x^{2}}} \ge \sqrt{12-2\sqrt{35+2x-x^{2}}}\)
При выполнении преобразований использованы следующие приемы и формулы:
- свойства арифметического квадратного корня:
\((\sqrt a)^2 = a\);
\(\sqrt a\cdot\sqrt b = \sqrt{ab}\);
\(\sqrt{a^2} = |a|\);
- квадрат разности двух выражений:
\((a - b)^2 = a^2 - 2ab + b^2\);
- разность квадратов двух выражений:
\((a - b)(a + b) = a^2 - b^2\);
- свойства модуля:
\(|a| = a\), при \(a \ge0\),
\(|a| = -a\), при \(a < 0\).
После преобразований получили
\( y=2\sqrt{6 - |x-1|}\).
Далее рассмотрели два случая:
\(x - 1 \ge 0\) и \(x - 1 < 0\).
В каждом случае подобрали такие целые значения \(x\), при которых \(y\) - целое число.
Вернуться к содержанию учебника