Упражнение 1115 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1115 учебника 2023-2025 (стр. 250):
Постройте график функции:
а) \(y = 1{,}6x;\)
б) \(y = -0{,}4x.\)
Перечислите свойства функции
\(y = kx\) при \(k > 0\) и при \(k < 0.\)
№1115 учебника 2013-2022 (стр. 255):
Найдите целые значения \(x\), при которых функция \[ y=\sqrt{\,20+2\sqrt{91+6x-x^{2}}\,}-\sqrt{\,20-2\sqrt{91+6x-x^{2}}\,} \] принимает целые значения.
Подсказка
№1115 учебника 2023-2025 (стр. 250):
Вспомните:
- Линейную функцию, ее график и свойства.
- Координаты точки.
- Числовые промежутки.
- Умножение десятичных дробей.
- Умножение рациональных чисел.
№1115 учебника 2013-2022 (стр. 255):
Вспомните:
- Целые числа.
- Арифметический квадратный корень.
- Свойства арифметического квадратного корня.
- Модуль числа.
- Квадрат разности двух выражений.
- Разность квадратов двух выражений.
- Решение неравенств с одной переменной.
- Раскрытие скобок.
- Сложение рациональных чисел.
Ответ
№1115 учебника 2023-2025 (стр. 250):
а) \(y = 1{,}6x\)
| \(x\) | 0 | 5 |
| \(y\) | 0 | 8 |
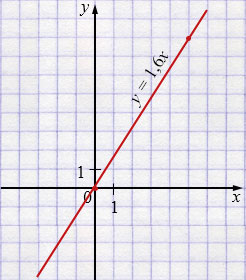
Свойства функции при \(k>0\):
1) \(D(y) = R\)
2) \(E(y) = R\)
3) \(y = 0\) при \(x = 0\)
4) \(y < 0\) при \(x < 0\),
\(y > 0\) при \(x > 0\)
5) Функция возрастает, так как \(k > 0\).
б) \(y = -0{,}4x\)
| \(x\) | 0 | 5 |
| \(y\) | 0 | -2 |

Свойства функции при \(k > 0\):
1) \(D(y) = R\)
2) \(E(y) = R\)
3) \(y = 0\) при \(x = 0\)
4) \(y < 0\) при \(x > 0\),
\(y > 0\) при \(x < 0\)
5) Функция убывает, так как \(k < 0\).
Пояснения:
Функцию \(y = kx\) называют прямой пропорциональностью. Графиком функции прямой пропорциональности является прямая, которая проходит через начало координат. График строят по двум точкам, так как прямая однозначно задается двумя точками, одна из них - точка \((0; 0)\).
1. Функция определена при любых значениях переменной \(x\), т.е.
\(D(y) = R\).
2. Значение функции может быть любое число, т.е. \(E(y) = R\).
3. Функция обращается в нуль при \(x =0\).
4. При \(k > 0\) функция принимает отрицательные значения на промежутке \((-\infty; 0)\) и положительные значения на промежутке \((0; +\infty)\).
При \(k < 0\) функция принимает отрицательные значения на промежутке \((0; +\infty)\) и положительные значения на промежутке \((-\infty; 0)\).
5. При \(k>0\) функция \(y = kx\) является возрастающей, а при \(k < 0\) - убывающей.
№1115 учебника 2013-2022 (стр. 255):
\( y=\sqrt{20+2\sqrt{91+6x-x^{2}}}-\sqrt{20-2\sqrt{91+6x-x^{2}}} \)
\(y\) и \(x\) - целые числа.
\( y^2=\left(\sqrt{20+2\sqrt{91+6x-x^{2}}}-\sqrt{20-2\sqrt{91+6x-x^{2}}}\right)^2 \)
\( y^2=\left(\sqrt{20+2\sqrt{91+6x-x^{2}}}\right)^2-2\sqrt{20+2\sqrt{91+6x-x^{2}}}\cdot\sqrt{20-2\sqrt{91+6x-x^{2}}}+\left(\sqrt{20-2\sqrt{91+6x-x^{2}}}\right)^2 \)
\( y^2=20+\cancel{2\sqrt{91+6x-x^{2}}}-2\sqrt{(20^2-(2\sqrt{91+6x-x^{2}})^2}+20-\cancel{2\sqrt{91+6x-x^{2}}} \)
\( y^2=40-2\sqrt{400-4\cdot(91+6x-x^{2})} \)
\( y^2=40-2\sqrt{400-364-24x+4x^{2}} \)
\( y^2=40-2\sqrt{36-24x+4x^{2}} \)
\( y^2=40-2\sqrt{4(9-6x+x^{2})} \)
\( y^2=40-2\cdot2\sqrt{(x-3)^{2}} \)
\( y^2=40-4|x-3| \)
\( y^2=4(10-|x-3|) \)
\(y \ge 0\)
\( y=\sqrt{4(10-|x-3|)} \)
\( y=2\sqrt{10-|x-3|} \)
1) Если \(x - 3 \ge 0\), то есть \(x \ge3\), то
\( y=2\sqrt{10-(x-3)} =\)
\(=2\sqrt{10 - x + 3} = 2\sqrt{13 - x} \)
Если \(x = 4\), то
\(y = 2\sqrt{13 - 4} = 2\sqrt{9} = 2\cdot3 = 6 \) - целое число.
Если \(x = 9\), то
\(y = 2\sqrt{13 - 9} = 2\sqrt{4} = 2\cdot2 = 4 \) - целое число.
Если \(x = 12\), то
\(y = 2\sqrt{13 - 12} = 2\sqrt{1} = 2\cdot1 = 2 \) - целое число.
Если \(x = 13\), то
\(y = 2\sqrt{13 - 13} = 2\sqrt{0} = 0 \) - целое число.
2) Если \(x - 3 < 0\), то есть \(x < 3\), то
\( y=2\sqrt{10+(x-3)} =\)
\(=2\sqrt{10+x - 3} =2\sqrt{7+x} \)
Если \(x = -7\), то
\(y = 2\sqrt{7+(-7)}= 2\sqrt0 = 0 \) - целое число.
Если \(x = -6\), то
\(y = 2\sqrt{7+(-6)}= 2\sqrt1 = 2\cdot1 = 2 \) - целое число.
Если \(x = -3\), то
\(y = 2\sqrt{7+(-3)}= 2\sqrt4 = 2\cdot 2 = 4 \) - целое число.
Ответ: \(-7; -6; -3; 4; 9; 12; 13.\)
Пояснения:
Левую и правую части функции возводим в квадрат, учитывая то, что \(y\ge0\), так как
\(\sqrt{20+2\sqrt{91+6x-x^{2}}}\ge\sqrt{20-2\sqrt{91+6x-x^{2}}} \).
При выполнении преобразований использованы следующие приемы и формулы:
- свойства арифметического квадратного корня:
\((\sqrt a)^2 = a\);
\(\sqrt a\cdot\sqrt b = \sqrt{ab}\);
\(\sqrt{a^2} = |a|\);
- квадрат разности двух выражений:
\((a - b)^2 = a^2 - 2ab + b^2\);
- разность квадратов двух выражений:
\((a - b)(a + b) = a^2 - b^2\);
- свойства модуля:
\(|a| = a\), при \(a \ge0\),
\(|a| = -a\), при \(a < 0\).
После преобразований получили
\( y=2\sqrt{10-|x-3|} \).
Далее рассмотрели два случая:
\(x - 3 \ge 0\) и \(x - 3 < 0\).
В каждом случае подобрали такие целые значения \(x\), при которых \(y\) - целое число.
Вернуться к содержанию учебника