Упражнение 1114 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1114 учебника 2023-2025 (стр. 250):
Постройте график функции и перечислите её свойства:
а) \(y = 1{,}5x - 3;\)
б) \(y = -0{,}6x + 5.\)
№1114 учебника 2013-2022 (стр. 254):
Найдите три различные обыкновенные дроби вида \(\dfrac{x}{x+1}\), сумма которых равна натуральному числу.
Подсказка
№1114 учебника 2023-2025 (стр. 250):
Вспомните:
- Линейную функцию, ее график и свойства.
- Координаты точки.
- Числовые промежутки.
- Сравнение рациональных чисел.
- Умножение десятичных дробей.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Деление десятичных дробей.
- Деление рациональных чисел.
- Сокращение дробей.
- Неправильные дроби.
- Смешанные числа.
№1114 учебника 2013-2022 (стр. 254):
Ответ
№1114 учебника 2023-2025 (стр. 250):
а) \(y = 1{,}5x - 3\)
| \(x\) | 0 | 2 |
| \(y\) | -3 | 0 |
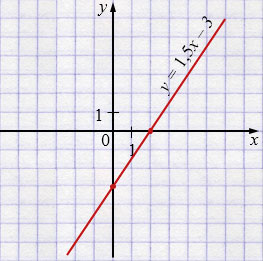
Свойства функции:
1) \(D(y) = R\)
2) \(E(y) = R\)
3) \(y = 0\) при \(x = 2\)
4) \(y < 0\) при \(x < 2\),
\(y > 0\) при \(x > 2\)
5) Функция возрастает, так как
\(k = 1,5 > 0\).
б) \(y = -0{,}6x + 5\)
| \(x\) | 0 | 5 |
| \(y\) | 5 | 2 |
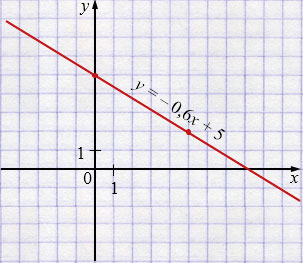
Свойства функции:
1) \(D(y) = R\)
2) \(E(y) = R\)
3) \(y = 0\) при
\(-0{,}6x + 5 = 0\)
\(-0{,}6x = -5\)
\(x = \frac{5}{0,6}\)
\(x = \frac{50}{6}\)
\(x = \frac{25}{3}\)
\(x =8\frac13\)
4) \(y < 0\) при \(x > 8\frac13\),
\(y > 0\) при \(x < 8\frac13\)
5) Функция убывает, так как
\(k = -0,6 < 0\).
Пояснения:
Функцию, которую можно задать формулой вида \(y = kx + b\), \(k\) и \(b\) - некоторые числа, \(x\) - независимая переменная, называют линейной. Графиком линейной функции является прямая. График строят по двум точкам, так как прямая однозначно задается двумя точками.
1. Функция определена при любых значениях переменной \(x\), т.е.
\(D(y) = R\).
2. Значение функции может быть любое число, т.е. \(E(y) = R\).
3. Функция обращается в нуль при \(x = -\frac{b}{k}\).
Это свойство вытекает из решения уравнения \(kx + b = 0\), откуда получаем \(kx = -b\), тогда \(x = -\frac{b}{k}\).
4. При \(k > 0\) функция принимает отрицательные значения на промежутке \((-\infty; -\frac{b}{k})\) и положительные значения на промежутке \((-\frac{b}{k}; +\infty)\).
При \(k < 0\) функция принимает отрицательные значения на промежутке \((-\frac{b}{k}; +\infty)\) и положительные значения на промежутке \((-\infty; -\frac{b}{k})\).
5. При \(k>0\) функция \(y = kx + b\) является возрастающей, а при \(k < 0\) - убывающей.
№1114 учебника 2013-2022 (стр. 254):
Пусть \(x_1, x_2, x_3\) такие, что сумма
\( \dfrac{x_1}{x_1+1}+\dfrac{x_2}{x_2+1}+\dfrac{x_3}{x_3+1} \) - натуральное число.
\(\dfrac{x_1}{x_1+1} < 1\), \(\dfrac{x_2}{x_2+1} < 1\),
\(\dfrac{x_3}{x_3+1} < 1\), так как дроби обыкновенные, значит
\( \dfrac{x_1}{x_1+1}+\dfrac{x_2}{x_2+1}+\dfrac{x_3}{x_3+1} < 3\)
Если \(x_1 = 1\), то \(\dfrac{x_1}{x_1+1} = \dfrac12,\)
Если \(x_1 = 2\), то \(\dfrac{x_1}{x_1+1} = \dfrac23.\)
\(\dfrac23 > \dfrac12\), значит, \(\dfrac{x_1}{x_1+1} > \dfrac12.\)
Аналогично,
\(\dfrac{x_2}{x_2+1} > \dfrac12\) и \(\dfrac{x_3}{x_3+1} >\dfrac12\).
Тогда
\( \dfrac{x_1}{x_1+1}+\dfrac{x_2}{x_2+1}+\dfrac{x_3}{x_3+1} > \dfrac12 + \dfrac12 + \dfrac12\)
\( \dfrac{x_1}{x_1+1}+\dfrac{x_2}{x_2+1}+\dfrac{x_3}{x_3+1} > \dfrac32\)
Получаем:
\( \dfrac32 < \dfrac{x_1}{x_1+1}+\dfrac{x_2}{x_2+1}+\dfrac{x_3}{x_3+1} < 3\)
Следовательно,
\(\dfrac{x_1}{x_1+1}+\dfrac{x_2}{x_2+1}+\dfrac{x_3}{x_3+1} = 2\) - натуральное число.
Пусть \(x_1 = 1\), \(x_2 = 2\)
\(\dfrac{1}{1+1}+\dfrac{2}{2+1}+\dfrac{x_3}{x_3+1} = 2\)
\(\dfrac{1}{2} ^{\color{blue}{\backslash3}} +\dfrac{2}{3} ^{\color{blue}{\backslash2}} +\dfrac{x_3}{x_3+1} = 2\)
\(\dfrac{3}{6} +\dfrac{4}{6} +\dfrac{x_3}{x_3+1} = 2\)
\(\dfrac{7}{6} + \dfrac{x_3}{x_3+1} = 2\)
\(\dfrac{x_3}{x_3+1} = 2 ^{\color{blue}{\backslash6}} - \dfrac{7}{6}\)
\(\dfrac{x_3}{x_3+1} = \dfrac{12}{6} - \dfrac{7}{6}\)
\(\dfrac{x_3}{x_3+1} = \dfrac{5}{6}\) при \(x_3 = 5\)
Ответ: \(\dfrac{1}{2}; \dfrac{2}{3}; \dfrac{5}{6}\).
Пояснения:
При решении используем то, что если почленно сложить верные неравенства одного знака, то получится верное неравенство.
Вернуться к содержанию учебника