Упражнение 844 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(4x(x+0,25) > (2x+3)(2x-3)\)

\(4x(x+0,25) -(2x+3)(2x-3) =\)

\(=4x^2+x - (4x^2-9) =\)

\(=4x^2+x - 4x^2+9 =\)

\(=x+9\) - зависит от \(x\).

Ответ: неверно.

б) \((5x-1)(5x+1) < 25x^2 + 2\)

\( (5x-1)(5x+1) - (25x^2+2) =\)

\(=25x^2-1 - 25x^2-2 =\)

\(=-3 < 0\)

Ответ: верно.

в) \((3x+8)^2 > 3x(x+16)\)

\( (3x+8)^2 - 3x(x+16) =\)

\(=9x^2+\cancel{48x}+64 - 3x^2-\cancel{48x} =\)

\(=6x^2+64 > 0\) при любом \(x\).

Ответ: верно.

г) \((7+2x)(7-2x) < 49 - x(4x+1)\)

\( (7+2x)(7-2x) - \bigl(49 - x(4x+1)\bigr) =\)

\(=(49-4x^2) - (49-4x^2-x) =\)

\(=\cancel{49}-\cancel{4x^2} - \cancel{49}+\cancel{4x^2}+x =\)

\(=x\) - зависит от \(x\).

Ответ: неверно.

Пояснения:

Для каждого неравенства вычислялась разность:

левая часть − правая часть.

Затем учитывали, то что:

- если \(a - b < 0\), то \(a < b\);

если \(a - b > 0\), то \(a > b\).

Если знак разности зависит от \(x\), то неравенство выполняется только при некоторых значениях переменной.

а) \(5(x - 1) + 7 \leq 1 - 3(x + 2)\)

\(5x - 5 + 7 \leq 1 - 3x - 6 \)

\(5x + 2 \leq -3x - 5 \)

\(5x + 3x \leq - 5 - 2 \)

\(8x \leq -7 \)   \(/ : 8\)

\(x \leq -\frac{7}{8}\)

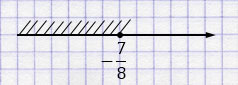
Ответ: \((-\infty; -\frac78]\).

б) \(4(a + 8) - 7(a - 1) < 12\)

\(4a + 32 - 7a + 7 < 12 \)

\(-3a + 39 < 12 \)

\(-3a < 12 - 39 \)

\(-3a < -27\)   \(/ : (-3)\)

\(a > 9\).

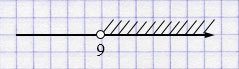
Ответ: \((9; +\infty)\).

в) \(4(b - 1,5) - 1,2 \geq 6b - 1\)

\(4b - 6 - 1,2 \geq 6b - 1 \)

\(4b - 7,2 \geq 6b - 1 \)

\(4b - 6b \geq - 1 + 7,2 \)

\(-2b \geq 6,2 \)   \(/ : (-2)\)

\(b \leq -3,1\).

Ответ: \((-\infty; -3,1]\).

г) \(1,7 - 3(1 - m) \leq -(m - 1,9)\)

\(1,7 - 3 + 3m \leq -m + 1,9 \)

\(3m - 1,3 \leq -m + 1,9 \)

\(3m + m \leq 1,9 + 1,3 \)

\(4m \leq 3,2 \)   \(/ :4\)

\(m \leq 0,8\).

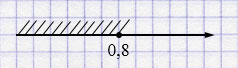
Ответ: \((-\infty; 0,8]\).

д) \(4x > 12(3x - 1) - 16(x + 1)\)

\(4x > 36x - 12 - 16x - 16 \)

\(4x > 20x - 28 \)

\(4x - 20x > - 28 \)

\(-16x > -28 \)   \( : (-16)\)

\(x < \frac{28}{16}\)

\(x < \frac{7}{4}\)

\(x < 1,75\)

Ответ: \((-\infty; 1,75)\).

е) \(a + 2 < 5(2a + 8) + 13(4 - a)\)

\(a + 2 < 10a + 40 + 52 - 13a \)

\(a + 2 < -3a + 92 \)

\(a + 3a < 92 - 2 \)

\(4a < 90 \)   \(/ : 4\)

\(a < 22,5\)

Ответ: \((-\infty; 22,5)\).

ж) \(6y - (y + 8) - 3(2 - y) \leq 2\)

\(6y - y - 8 - 6 + 3y \leq 2 \)

\(8y - 14 \leq 2\)

\(8y \leq 2 + 14\)

\(8y \leq 16 \)   \(/ : 8\)

\(y \leq 2\).

Ответ: \((-\infty; 2]\).

Пояснения:

При решении неравенств сначала раскрываем скобки, используя распределительное свойство умножения, и приводим подобные слагаемые.

Затем при решении неравенств используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.