Упражнение 836 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(y = kx + b\)

\((-1; 3)\), \((2; -2)\):

\( \begin{cases} -k + b = 3, \\ 2k + b = -2  /\times(-1) \end{cases} \)

\( \begin{cases} -k + b = 3, \\ -2k - b = 2 \end{cases} \)  \((+)\)

\( \begin{cases} -3k = 5, \\ -2k - b = 2 \end{cases} \)

\( \begin{cases} k = -\frac53, \\ -2k - b = 2 \end{cases} \)

\( \begin{cases} k = -1\frac23, \\ -2\cdot(-\frac53) - b = 2 \end{cases} \)

\( \begin{cases} k = -1\frac23, \\ -2\cdot(-\frac53) - b = 2 \end{cases} \)

\( \begin{cases} k = -1\frac23, \\ \frac{10}{3} - b = 2 \end{cases} \)

\( \begin{cases} k = -1\frac23, \\ b = \frac{10}{3} - 2 \end{cases} \)

\( \begin{cases} k = -1\frac23, \\ b = 3\frac{1}{3} - 2 \end{cases} \)

\( \begin{cases} k = -1\frac23, \\ b = 1\frac{1}{3} - 2 \end{cases} \)

\(y = -1\frac{{2}}{3}x + 1\frac13\)

Ответ: \(y = -1\frac{{2}}{3}x + 1\frac13\).

б) \(y = kx + b\)

\((4; 1)\), \((-3; -1)\):

\( \begin{cases} 4k + b = 1, \\ -3k + b = -1  /\times(-1) \end{cases} \)

\( \begin{cases} 4k + b = 1, \\ 3k - b = 1 \end{cases} \)  \((+)\)

\( \begin{cases} 7k = 2, \\ 3k - b = 1 \end{cases} \)

\( \begin{cases} k = \frac27, \\ 3\cdot\frac27 - b = 1 \end{cases} \)

\( \begin{cases} k = \frac27, \\ \frac67 - b = 1 \end{cases} \)

\( \begin{cases} k = \frac27, \\ b = \frac67 - 1 \end{cases} \)

\( \begin{cases} k = \frac27, \\ b = -\frac17 \end{cases} \)

\(y = \frac{{2}}{7}x - \frac17\)

Ответ: \(y = \frac{{2}}{7}x - \frac17\).

в) \(y = kx + b\)

\((0; 5)\), \((4; 0)\):

\( \begin{cases} 0\cdot k + b= 5, \\ 4k + b=0 \end{cases} \)

\( \begin{cases} b = 5, \\ 4k + 5=0 \end{cases} \)

\( \begin{cases} b = 5, \\ 4k =-5 \end{cases} \)

\( \begin{cases} b = 5, \\ 4k =-\frac54 \end{cases} \)

\( \begin{cases} b = 5, \\ k =-1,25 \end{cases} \)

\(y = -1,25x + 5\)

Ответ: \(y = -1,25x + 5\).

г) \(y = kx + b\)

\((-3; 0)\), \((0; -6)\):

\( \begin{cases} -3k + b=0, \\ 0\cdot k + b=-6 \end{cases} \)

\( \begin{cases} -3k + -6=0, \\ b=-6 \end{cases} \)

\( \begin{cases} -3k =6, \\ b=-6 \end{cases} \)

\( \begin{cases} k =-\frac63, \\ b=-6 \end{cases} \)

\( \begin{cases} k =-2, \\ b=-6 \end{cases} \)

\(y = -2x - 6\)

Ответ: \(y = -2x - 6\).

Пояснения:

Общий вид линейной функции:

\(y = kx + b\).

Так как прямая проходит через две точки, подставляем их координаты и получаем систему уравнений относительно \(k\) и \(b\).

В пунктах а) и б) системы решали способом сложения, пунктах в) и г) - способом подстановки.

а) \(3x > 15 \)   \( /:3\)

\(x > 5\).

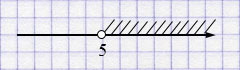
Ответ: \((5; +\infty)\).

б) \(-4x < -16 \)   \( /:(-4)\)

\(x > 4\)

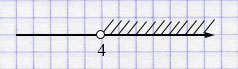
Ответ: \((4; +\infty)\).

в) \(-x \geq 1\)    \(/\times(-1)\)

\(x \leq -1\).

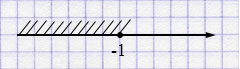
Ответ: \((-\infty; -1]\).

г) \(11y \leq 33 \)  \(/ :11\)

\(y \leq 3\).

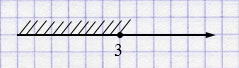
Ответ: \((-\infty; 3]\).

д) \(12y < 1,8\)   \(/ : 12\)

\(y < 0,15\).

Ответ: \((-\infty; 0,15)\).

е) \(27b \geq 12\)   \(/ : 27\)

\(b \geq \frac{12}{27} \)

\(b \geq \frac{4}{9}\).

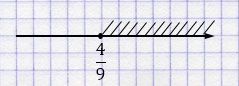
Ответ: \([\frac{4}{9}; +\infty)\).

ж) \(-6x > 1,5 \)   \(/ : (-6)\)

\(x < -0,25\).

Ответ: \((-\infty; -0,25)\).

з) \(15x \leq 0 \)   \(/ : 15\)

\(x \leq 0\).

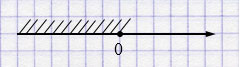
Ответ: \((-\infty; 0]\).

и) \(0,5y > -4\)    \(/ : 0,5\)

\(y > -8\).

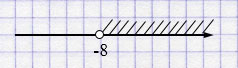
Ответ: \((-8; +\infty)\).

к) \(2,5a > 0 \)    \(/ : 2,5\)

\(a > 0\).

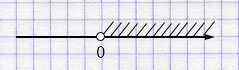
Ответ: \((0; +\infty)\).

л) \(\frac{1}{3}x > 6 \)    \(/\times3\)

\(x > 18\).

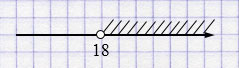
Ответ: \((18; +\infty)\).

м) \(-\frac{1}{7}y < -1 \)    \(/\times(-7)\)

\(y > 7\).

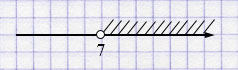
Ответ: \((7; +\infty)\).

Пояснения:

При решении рассматриваемых неравенств нужно делить обе части на коэффициент при переменной или умножать на знаменатель дроби при переменной. При этом помним:

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.