Упражнение 835 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\( \begin{cases} 5x - 2y = 3, \\ 10x - 4y = c \end{cases} \)

\( \begin{cases} 2y = 5x - 3, / : 2 \\ 4y = 10x - c / : 4 \end{cases} \)

\( \begin{cases} y = \frac52x - \frac32,\\ y = \frac{10}{4}x - \frac c4 \end{cases} \)

\( \begin{cases} y =2,5x - 1,5,\\ y = 2,5x - \frac c4 \end{cases} \)

а) Система имеет бесконечное множество решений при \(c = 6\).

б) Система не имеет решений при любом \(c \neq 6\).

Пояснения:

Уравнения приводим к виду

\(y=kx+b\).

Если для двух уравнений системы:

\(1)\;k_1=k_2,\;b_1\ne b_2\) — прямые параллельны, система не имеет решений.

\(2)\;k_1=k_2,\;b_1=b_2\) — прямые совпадают, система имеет бесконечно много решений.

а) \(x + 8 > 0\)

\(x > -8\).

Ответ: \((-8; +\infty)\).

б) \(x - 7 < 0\)

\(x < 7\).

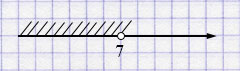
Ответ: \((-\infty; 7)\).

в) \(x + 1,5 \leq 0 \)

\(x \leq -1,5\).

Ответ: \((-\infty; -1,5]\).

г) \(x - 0,4 \geq 0 \)

\(x \geq 0,4\).

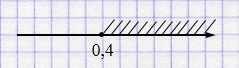
Ответ: \([0,4; +\infty)\).

Пояснения:

Неравенства вида

\(x + a > 0\) или \(x - a < 0\), 

\(x + a \geq 0\) или \(x - a \leq 0\), 

решаются переносом числа в правую часть с противоположным знаком.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.