Упражнение 1134 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1134 учебника 2023-2025 (стр. 224):
Две бригады должны были по плану изготовить за месяц 680 деталей. Первая бригада перевыполнила месячное задание на 20 %, а вторая — на 15 %, и поэтому обеими бригадами было изготовлено сверх плана 118 деталей. Сколько деталей должна была изготовить по плану каждая бригада за месяц?
№1134 учебника 2013-2022 (стр. 226):
Какую фигуру на координатной плоскости задаёт система неравенств:
а) \( \begin{cases} y \le x,\\ y \ge 7; \end{cases} \)
б) \( \begin{cases} y \le -x + 7,\\ y \ge -x + 1. \end{cases} \)
Подсказка
№1134 учебника 2023-2025 (стр. 224):
Вспомните:
- Решение задач с помощью системы уравнений.
- Что называют решением системы уравнений.
- Способ сложения при решении систем уравнений.
- Линейное уравнение.
- Деление и дроби.
- Свойства уравнений.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Подобные слагаемые.
№1134 учебника 2013-2022 (стр. 226):
Вспомните:
- Что называют решением системы неравенств с двумя переменными.
- График линейной функции.
- Координаты точки.
- Сложение рациональных чисел.
- Что называют углом.
Ответ
№1134 учебника 2023-2025 (стр. 224):
20% = 0,2;
15% = 0,15.
Пусть \(x\) плановое число деталей первой бригады, а \(y\) — второй.
Составим систему уравнений:
\( \begin{cases} x + y = 680,\\ 0{,}2x + 0{,}15y = 118 /\ : (-0,2) \end{cases} \)
\( \begin{cases} x + y = 680,\\ -x - 0{,}75y =- 590 \end{cases} \)
\( \begin{cases} 0,25y = 90,\\ x + y = 680 \end{cases} \)
\( \begin{cases} y = \frac{90}{0,25},\\ x = 680 - y \end{cases} \)
\( \begin{cases} y = \frac{9000}{25},\\ x = 680 - y \end{cases} \)
\( \begin{cases} y = 360,\\ x = 680 - 360 \end{cases} \)
\( \begin{cases} y = 360,\\ x = 320 \end{cases} \)
Ответ: 320 деталей должна была изготовить первая бригада по плану, 360 деталей - вторая.
Пояснения:
Использованные приёмы:
1) Введение переменных для плановых объёмов: \(x\) и \(y\).
2) Составление системы по сумме планов и сумме фактического выпуска с учётом процента перевыполнения.
3) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.
4) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.
5) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).
6) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
№1134 учебника 2013-2022 (стр. 226):
а) \( \begin{cases} y \le x,\\ y \ge 7; \end{cases} \)
\(y = x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
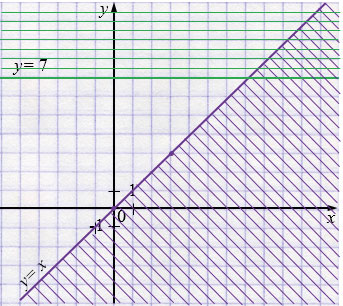
Ответ: угол.
б) \( \begin{cases} y \le -x + 7,\\ y \ge -x + 1. \end{cases} \)
\(y = -x + 7\)
| \(x\) | 0 | 7 |
| \(y\) | 7 | 0 |
\( y = -x + 1\)
| \(x\) | 0 | 1 |
| \(y\) | 1 | 0 |
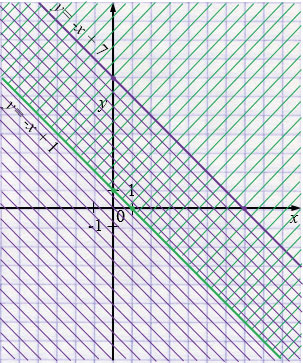
Ответ: полоса.
Пояснения:
Основные понятия и правила:
– Линейная функция \(y=kx+b\). Строится по двум точкам.
– Если прямые параллельны, пересечение задаёт полосу (между ними).
– Если прямые пересекаются, пересечение полуплоскостей даёт угол (с вершиной в точке пересечения).
Пояснения к случаю а):
– Линии \(y=x\) и \(y=7\) пересекаются в точке \( (7,7)\).
– Полуплоскость \(y\ge7\) лежит выше (или на) прямой \(y=7\), а \(y\le x\) — ниже (или на) прямой \(y=x\).
– Пересечение двух полуплоскостей ограничено двумя лучами, исходящими из точки \( (7,7)\), что дает угол.
Пояснения к случаю б):
– Прямые \(y=-x+7\) и \(y=-x+1\) параллельны.
– Полуплоскость \(y \le -x + 7\) лежит ниже (или на) прямой \(y = -x + 7\), а \(y \ge -x + 1\) — выше (или на) прямой \(y = -x + 1\).
– Пересечение двух полуплоскостей ограничено двумя параллельными прямыми, что дает полосу.
Вернуться к содержанию учебника