Задание 379 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№379 учебника 2013-2022 (стр. 104):
Из вершин В и D параллелограмма АВСD, у которого АВ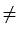 ВС и угол А острый, проведены перпендикуляры ВК и DМ к прямой АС. Докажите, что четырехугольник ВМDК - параллелограмм.
ВС и угол А острый, проведены перпендикуляры ВК и DМ к прямой АС. Докажите, что четырехугольник ВМDК - параллелограмм.
№379 учебника 2023-2024 (стр. 110):
Подсказка
№379 учебника 2013-2022 (стр. 104):
Вспомните:
- Какая фигура называется четырехугольником.
- Какой четырехугольник называется параллелограммом.
- Признаки параллелограмма.
- Какой угол называется острым.
- Что такое перпендикуляр к прямой.
- Признаки равенства прямоугольных треугольников.
- Теорему о накрест лежащих углах.
№379 учебника 2023-2024 (стр. 110):
Вспомните:
- Что такое ось симметрии фигуры.
- Что такое отрезок.
- Что называют серединным перпендикуляром к отрезку.
- Как построить серединный перпендикуляр к отрезку.
- Что такое угол.
- Что называют биссектрисой угла.
- Как построить биссектрису угла.
- Что называют треугольником.
- Какой треугольник называют равнобедренным, равносторонним.
- Свойства равнобедренного (равностороннего) треугольника.
Ответ
№379 учебника 2013-2022 (стр. 104):




№379 учебника 2023-2024 (стр. 110):
а) АВ - отрезок.
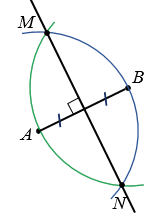
МN - ось симметрии отрезка АВ.
б) Угол hk
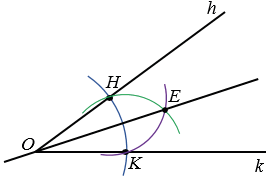
ОЕ - ось симметрии угла hk.
в) 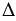 АВС - равнобедренный треугольник с основанием ВС.
АВС - равнобедренный треугольник с основанием ВС.
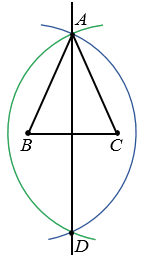
АD - ось симметрии равнобедренного  АВС.
АВС.
г) 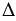 ЕDF - разносторонний.
ЕDF - разносторонний.
Разносторонний треугольник не имеет осей симметрии.
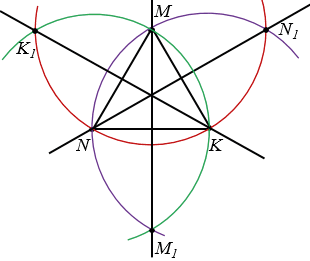
д) 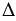 МNK - равносторонний.
МNK - равносторонний.
ММ1, NN1 и KK1 - оси симметрии равностороннего  МNK.
МNK.
Пояснения:
 , если для каждой точки фигуры симметричная ей точка относительно прямо
, если для каждой точки фигуры симметричная ей точка относительно прямо 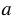 также принадлежит этой фигуре. Прямая
также принадлежит этой фигуре. Прямая 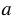 называется осью симметрии фигуры.
называется осью симметрии фигуры.а) У отрезка осью симметрии является серединный перпендикуляр к этому отрезку.
Нам дан отрезок АВ, чтобы построить серединный перпендикуляр к этому отрезку, строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно). Эти окружности пересекутся в двух точках М и N. Прямая МN - серединный перпендикуляр к отрезку АВ, а значит, и ось симметрии этого отрезка.

б) У неразвёрнутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла.
Нам дан угол hk, чтобы построить биссектрису этого угла, сначала строим окружность произвольного радиуса с центром в вершине О данного угла (полностью окружность строить необязательно). Эта окружность пересечет стороны угла hk в двух точках Н и К. Затем строим две окружности с центрами в точках Н и К радиуса НК (полностью окружности строить необязательно). Эти окружности пересекутся в точке Е. Прямая ОЕ и будет осью симметрии угла hk.

в) Равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии - это прямая, на которой расположена медиана (биссектриса, высота), проведенная к основанию (у равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию совпадают).
Нам дан равнобедренный 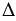 АВС с основанием ВС. Чтобы построить его ось симметрии, строим две окружности с центрами в точках В и С радиуса ВА (полностью окружности строить необязательно). Эти окружности пересекутся в двух точках А и D. Прямая АD - ось симметрии равнобедренного
АВС с основанием ВС. Чтобы построить его ось симметрии, строим две окружности с центрами в точках В и С радиуса ВА (полностью окружности строить необязательно). Эти окружности пересекутся в двух точках А и D. Прямая АD - ось симметрии равнобедренного 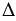 АВС с основанием ВС.
АВС с основанием ВС.

г) Разносторонний треугольник осей симметрии не имеет.

д) Равносторонний треугольник имеет три оси симметрии - это прямые, на которых расположены медианы (высоты, биссектрисы) этого треугольника (у равностороннего треугольника медианы, биссектрисы и высоты, проведенные из одной вершины совпадают).
Нам дан равносторонний 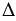 МNK. Чтобы построить оси симметрии этого равностороннего треугольника строим три окружности с центрами в точках М, N и K радиуса NM (полностью окружности строить необязательно). Каждая пара окружностей пересекутся в двух точках М и М1, N и N1, K и K1. Прямые ММ1, NN1 и KK1 - оси симметрии равностороннего
МNK. Чтобы построить оси симметрии этого равностороннего треугольника строим три окружности с центрами в точках М, N и K радиуса NM (полностью окружности строить необязательно). Каждая пара окружностей пересекутся в двух точках М и М1, N и N1, K и K1. Прямые ММ1, NN1 и KK1 - оси симметрии равностороннего 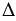 МNK.
МNK.

Вернуться к содержанию учебника