Построение биссектрисы угла

Пример:

Построить биссектрису данного угла.

Дано: А.

Построить: биссектрису А.

Решение:

Произвольно строим с помощью линейки А.

С помощью циркуля строим окружность произвольного радиуса с центром в вершине А.

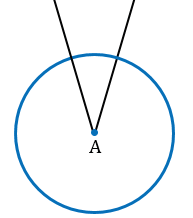
Точки пересечения данной окружности со сторонами А обозначим В и С.

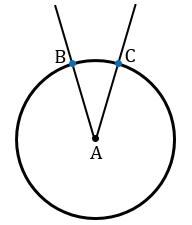
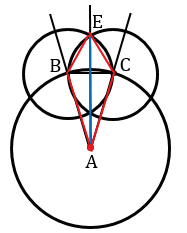
Теперь проведем две окружности одинакового радиуса ВС с центрами в точках В и С.

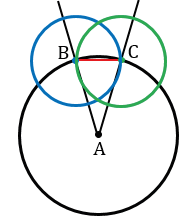
В зависимости от длины ВС, получим одну или две точки пересечения данных окружностей внутри А. Ту точку, которая лежит внутри угла обозначают буквой и проводят через нее луч с началом в точке А. В нашем случае, получилось две точки пересечения данных окружностей, которые лежат внутри А. Обозначаем одну из них Е и проводим с помощью линейки луч АЕ.

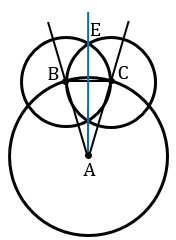
Докажем, что луч АЕ является биссектрисой данного А. Рассмотрим треугольники АВЕ и АСЕ.

В данных треугольниках АВ = АС как радиусы окружности с центром в точке А, ВЕ = СЕ по построению, АЕ - общая, следовательно, 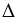АВЕ =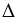АСЕ по 3 признаку равенства треугольников, откуда следует, что ВАЕ =САЕ, т.е луч АЕ - биссектриса данного А. Что и требовалось доказать.

Замечание:

• С помощью циркуля и линейки можно разделить данный угол на два равных угла, для этого нужно провести его биссектрису.
• С помощью циркуля и линейки можно разделить данный угол на четыре равных угла, для этого нужно разделить угол пополам (на два равных угла), а затем каждую половину разделить пополам еще раз.
• С помощью циркуля и линейки нельзя разделить данный угол на три равных угла (задача о трисекции угла).