Задание 378 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№378 учебника 2013-2022 (стр. 103):
Докажите, что параллелограмм является выпуклым четырехугольником.
№378 учебника 2023-2024 (стр. 110):
Подсказка
№378 учебника 2013-2022 (стр. 103):
Вспомните:
- Какая фигура называется многоугольником.
- Какой многоугольник называется выпуклым.
- Какая фигура называется параллелограммом.
№378 учебника 2023-2024 (стр. 110):
Вспомните:
- Что такое треугольник.
- Какие точки называют симметричными относительно прямой.
- Перпендикуляр к прямой.
- Измерение длины.
- Измерение углов.
Ответ
№378 учебника 2013-2022 (стр. 103):
Решение данной задачи приведено в учебнике на странице 104.
№378 учебника 2023-2024 (стр. 110):
1)
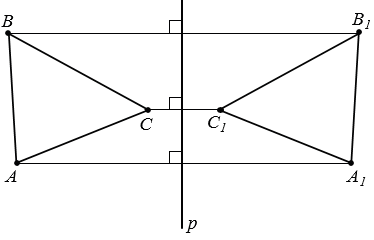
АВ = А1В1, АС = А1С1, ВС = В1С1
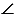 А =
А = 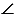 А1,
А1, 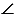 В =
В = 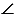 В1,
В1, 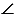 С =
С = 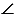 С1.
С1.
2)
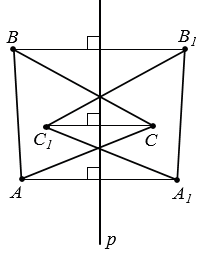
АВ = А1В1, АС = А1С1, ВС = В1С1
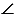 А =
А = 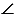 А1,
А1, 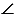 В =
В = 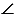 В1,
В1, 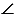 С =
С = 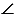 С1.
С1.
Пояснения:
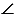 А =
А = 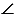 А1,
А1, 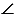 В =
В = 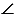 В1,
В1, 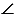 С =
С = 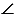 С1.
С1.Вернуться к содержанию учебника