Построение середины отрезка
Пример:
Построить середину данного отрезка.
Дано: отрезок АВ.
Построить: середину АВ.
Решение:
Строим с помощью линейки произвольный отрезок АВ.

Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.
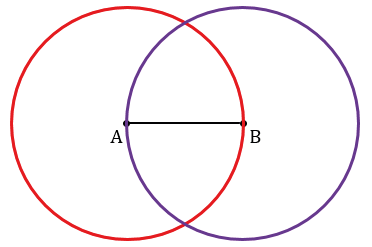
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.
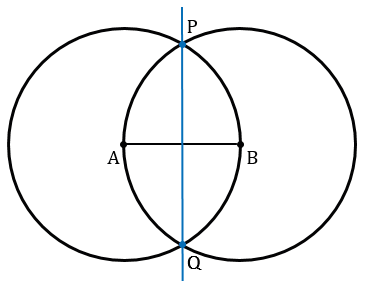
Точку пересечения прямой РQ и отрезка АВ обозначим О.
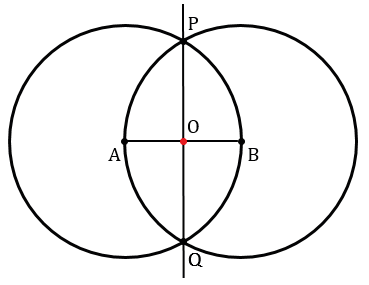
Докажем, что точка О - искомая точка, т.е. точка О - середина отрезка АВ.
Рассмотрим треугольники РАQ и РВQ.
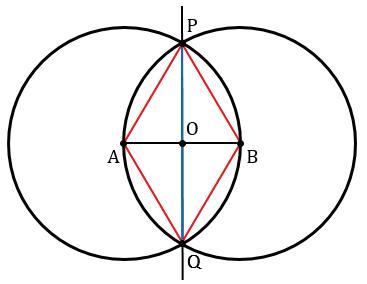
По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ - общая, следовательно,  РАQ =
РАQ = РВQ по 3 признаку равенства треугольников. Значит, по свойству равных треугольников
РВQ по 3 признаку равенства треугольников. Значит, по свойству равных треугольников 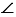 АРО =
АРО =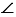 ВРО, тогда РО - биссектриса
ВРО, тогда РО - биссектриса  АРВ.
АРВ.
В  АРВ АР = ВР (как радиусы одинаковых окружностей), следовательно,
АРВ АР = ВР (как радиусы одинаковых окружностей), следовательно,  АРВ - равнобедренный, тогда по свойству равнобедренного треугольника биссектриса РО
АРВ - равнобедренный, тогда по свойству равнобедренного треугольника биссектриса РО  АРВ и его медиана, следовательно, точка О - середина отрезка АВ. Что и требовалось доказать.
АРВ и его медиана, следовательно, точка О - середина отрезка АВ. Что и требовалось доказать.
Советуем посмотреть:
Построение угла, равного данному
Построение перпендикулярных прямых
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 154, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 292, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 295, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 353, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 413, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 416, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 711, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 737, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 27, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник