Числовые множества
Все натуральные числа образуют множество натуральных чисел. Данное множество обозначается буквой N.
Все натуральные числа, противоположные им числа и число нуль образуют множество целых чисел. Данное множество обозначают буквой Z.
Множество натуральных чисел является подмножеством множества целых чисел, то есть N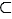 Z.
Z.
Целые и дробные (как положительные, так и отрицательные) числа образуют множество рациональных чисел. Данное множество обозначают буквой Q. Очевидно, что Z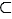 Q.
Q.
С помощью диаграмм Эйлера соотношение между множествами N, Z и Q будет изображено так:
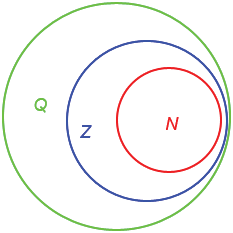
Название "рациональное число" связано с тем, что одним из значений латинского слова ratio является "отношение", а каждое рациональное число можно представить в виде отношения 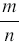 , где
, где 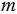 - целое число, а
- целое число, а 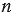 - натуральное. Поделив числитель данной дроби на ее знаменатель, можно представить данное рациональное число в виде конечной десятичной дроби или бесконечной периодической десятичной дроби (при этом повторяющуюся группу чисел называют периодом дроби и записывают в круглых скобках). Мы помним, что справа от конечной десятичной дроби мы можем записывать сколько угодно нулей, а значит, любую десятичную дробь мы можем записать в виде периодической десятичной дроби с периодом 0.
- натуральное. Поделив числитель данной дроби на ее знаменатель, можно представить данное рациональное число в виде конечной десятичной дроби или бесконечной периодической десятичной дроби (при этом повторяющуюся группу чисел называют периодом дроби и записывают в круглых скобках). Мы помним, что справа от конечной десятичной дроби мы можем записывать сколько угодно нулей, а значит, любую десятичную дробь мы можем записать в виде периодической десятичной дроби с периодом 0.
Вывод:
Каждое рациональное число можно представить в виде бесконечной периодической дроби.
Каждая бесконечная периодическая десятичная дробь является записью некоторого рационального числа.
Рассмотрим уравнение 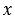 2 = 3. Так как 3>0, то это уравнение имеет два корня:
2 = 3. Так как 3>0, то это уравнение имеет два корня: 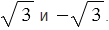
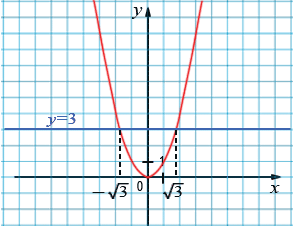
Но не существует рационального числа, квадрат которого равен 3, то есть числа 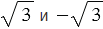 не являются рациональными. Эти числа являются примерами иррациональных чисел (приставка "ир" означает отрицание). Иррациональные числа могут быть представлены в виде бесконечных непериодических десятичных дробей.
не являются рациональными. Эти числа являются примерами иррациональных чисел (приставка "ир" означает отрицание). Иррациональные числа могут быть представлены в виде бесконечных непериодических десятичных дробей.
Объединение множеств иррациональных и рациональных чисел называют множеством действительных чисел, данное множество обозначают буквой R, при этом:
N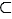 Z
Z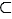 Q
Q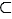 R.
R.
Иллюстрацией связи между числовыми множествами, которые рассмотрены выше, может служить схема:
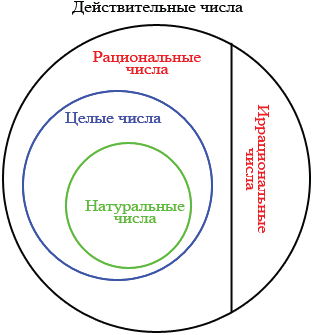
Над действительными числами можно выполнять четыре арифметических действия: сложение, вычитание, умножение, деление (кроме деления на ноль). Результатом данных действий будет действительное число. Заметим, что из любого неотрицательного действительного числа можно извлечь квадратный корень, причем в результате мы получим также действительное число.
При сравнении действительных чисел помним, что:
Любое положительное действительное число больше нуля и любого отрицательного действительного числа.
Любое отрицательное действительное число меньше нуля.
Из двух отрицательных действительных чисел больше то, у которого модуль меньше.
Советуем посмотреть:
Подмножество. Операции над множествами. Объединение и пересечение множеств
Правило встречается в следующих упражнениях:
8 класс
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 470, Мерзляк, Полонский, Якир, Учебник
Номер 480, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 534, Мерзляк, Полонский, Якир, Учебник
Номер 586, Мерзляк, Полонский, Якир, Учебник
Номер 740, Мерзляк, Полонский, Якир, Учебник
Упражнение 268, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 449, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс