Средняя линия треугольника

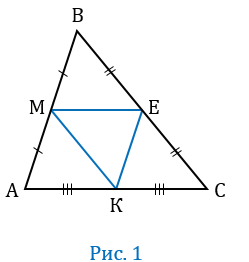
Средняя линия треугольника - отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 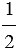. На рисунке 1 изображен треугольник АВС, отрезки МЕ, МК и КЕ являются средними линиями данного треугольника, ВМЕ =АМК =СЕК =МЕК.

Теорема

Доказательство

Дано: АВС, МЕ - средняя линия.

Доказать: МЕ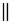АС, МЕ = 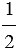АС.

Доказательство:

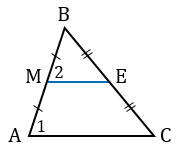
В треугольниках МВЕ и АВС:

• В - общий;
• ВА = 2ВМ, т.к. МЕ - средняя линия, значит, М - середина АВ, тогда 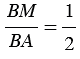, аналогично, 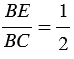, т.е. .

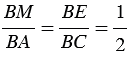Следовательно, треугольники МВЕ и АВС подобны (по 2 признаку подобия треугольников), поэтому 1 =2 и .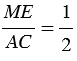

Прямые МЕ и АС пересечены секущей АВ, углы 1 и 2 - соответственные, при этом 1 =2, следовательно, МЕАС (по признаку параллельности двух прямых).

Из равенства 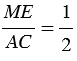следует, что МЕ = 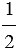АС. Теорема доказана.

Задача:

Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.

Дано: АВС, АА₁ и ВВ₁, СС₁ - медианы, АА₁ВВ₁ = О.

Доказать: АА₁ВВ₁СС₁ = О, АО : ОА₁ = ВО : ОВ₁ = СО : ОС₁ = 2 : 1.

Доказательство:

Проведем среднюю линию В₁А₁ треугольника АВС (В₁А₁ - средняя линия, т.к. по условию АА₁ и ВВ₁ - медианы, значит точки А₁ и В₁ - середины сторон АС и СВ).

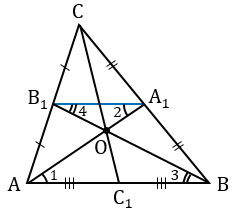
А₁В₁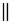АВ (по теореме, доказанной выше), АА₁ и ВВ₁ - секущие, 1 и 2, 3 и 4 - накрест лежащие, значит, 1 =2, 3 =4 (по теореме о накрест лежащих углах). Следовательно, треугольники АОВ и А₁ОВ₁ подобны (по 1 признаку подобия), тогда сходственные стороны данных треугольников пропорциональны:

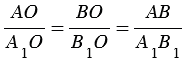.      (1)

Так как А₁В₁ - средняя линия, А₁В₁ = 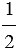АВ, откуда АВ = 2А₁В₁, поэтому АО = 2А₁О и ВО = 2В₁О. Подставляя три последних равенства в (1), получим:

.

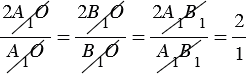Следовательно, точка О, в которой пересекаются медианы АА₁ и ВВ₁ делит каждую из них в отношении 2 : 1, считая от вершины.

Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2 : 1, считая от вершины, и, значит, совпадает с точкой О.

Итак, все три медианы АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины. Что и требовалось доказать.