Третий признак подобия треугольников
Теорема
| Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны |
Доказательство
Дано: 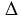 АВС и
АВС и 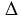 А1В1С1,
А1В1С1, 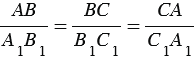
Доказать: 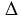 АВС
АВС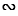
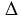 А1В1С1
А1В1С1
Доказательство:
Рассмотрим 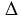 АВС и
АВС и 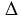 А1В1С1, у которых
А1В1С1, у которых 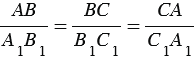 (1)
(1)
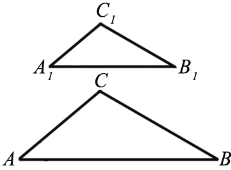
Для доказательства теоремы, учитывая второй признак подобия треугольников, достаточно доказать, что 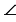 А =
А = 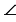 А1.
А1.
Рассмотрим 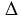 АВС2, у которого
АВС2, у которого 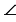 1 =
1 = 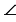 А1,
А1, 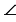 2 =
2 =  В1.
В1.
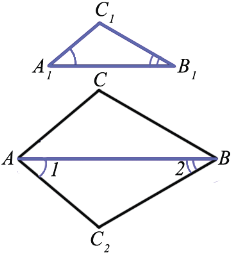
 АВС2
АВС2
 А1В1С1 по первому признаку подобия треугольников, поэтому
А1В1С1 по первому признаку подобия треугольников, поэтому 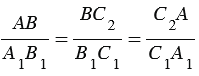 (2).
(2).
Сравнивая равенства (1) и (2), получаем: ВС = ВС2, СА =С2А.  АВС =
АВС = АВС2 по трем сторонам. Отсюда следует, что
АВС2 по трем сторонам. Отсюда следует, что 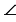 А =
А = 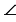 1, а так как
1, а так как 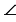 1 =
1 = 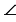 А1, то
А1, то 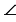 А =
А = 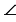 А1. Теорема доказана.
А1. Теорема доказана.
Советуем посмотреть:
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Правило встречается в следующих упражнениях:
7 класс
Задание 560, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 613, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 626, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник