Признаки параллельности двух прямых
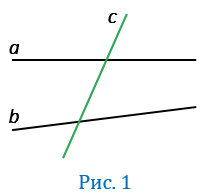
Рассмотрим две прямые 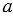 и
и 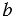 , которые пересекает в двух точках третья прямая
, которые пересекает в двух точках третья прямая 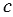 (Рис.1). Прямая
(Рис.1). Прямая 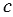 называется секущей по отношению к прямым
называется секущей по отношению к прямым 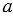 и
и 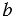 .
.
При пересечении прямых 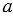 и
и 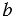 секущей
секущей 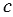 образуется восемь углов, которые обозначены цифрами на Рис.2.
образуется восемь углов, которые обозначены цифрами на Рис.2.
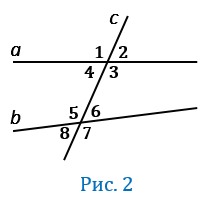
Некоторые пары из этих углов имеют специальные названия:
накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Признаки параллельности двух прямых
1. Теорема
| Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. |
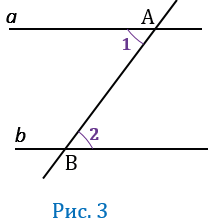
Дано: прямые 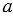 и
и 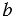 , АВ - секущая,
, АВ - секущая,  1 и
1 и  2 - накрест лежащие,
2 - накрест лежащие,  1 =
1 =  2 (Рис.3).
2 (Рис.3).
Доказать: 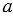
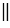
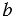 .
.
Доказательство:
1 случай
Предположим, что  1 =
1 =  2 = 900, т.е. эти углы прямые, получим
2 = 900, т.е. эти углы прямые, получим 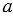
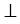 АВ и
АВ и 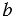
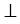 АВ (Рис.4), следовательно,
АВ (Рис.4), следовательно, 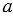
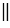
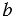 (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны).
(т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны).
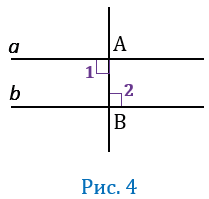
2 случай
Предположим, что  1 и
1 и  2 - не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой
2 - не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой 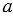 и продолжим его до пересечения с прямой
и продолжим его до пересечения с прямой 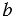 , точку пересечения ОН с прямой
, точку пересечения ОН с прямой 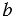 обозначим Н1 (Рис. 5).
обозначим Н1 (Рис. 5).
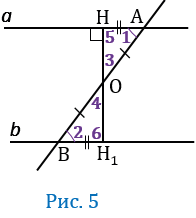
Получим 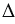 ОНА =
ОНА = 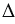 ОН1В по 2 признаку равенства треугольников (углы 3 и 4 вертикальные, т.к. получены при пересечении двух прямых АВ и НН1, а вертикальные углы равны друг другу, т.е.
ОН1В по 2 признаку равенства треугольников (углы 3 и 4 вертикальные, т.к. получены при пересечении двух прямых АВ и НН1, а вертикальные углы равны друг другу, т.е.  3 =
3 =  4, АО = ОВ, т.к. О - середина АВ,
4, АО = ОВ, т.к. О - середина АВ,  1 =
1 =  2 по условию), следовательно,
2 по условию), следовательно,  5 =
5 = 6, значит,
6, значит,  6 - прямой, также как и
6 - прямой, также как и  5 (т.к по построению ОН
5 (т.к по построению ОН 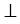
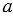 ).
).
Получаем, НН1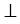
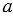 и НН1
и НН1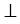
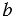 , значит
, значит 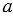
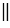
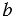 (т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны). Что и требовалось доказать.
(т.к. две прямые перпендикулярные к третьей прямой не пересекаются, т.е. параллельны). Что и требовалось доказать.
2. Теорема
| Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. |
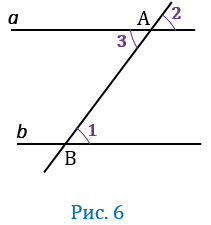
Дано: прямые 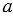 и
и 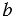 , АВ - секущая,
, АВ - секущая,  1 и
1 и  2 - соответственные,
2 - соответственные,  1 =
1 =  2 (Рис.6).
2 (Рис.6).
Доказать: 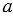
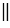
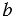 .
.
Доказательство:
По условию  1 =
1 =  2 и
2 и  2 =
2 =  3, т.к.они вертикальные, откуда
3, т.к.они вертикальные, откуда  1 =
1 =  3, при этом углы 1 и 3 накрест лежащие, следовательно,
3, при этом углы 1 и 3 накрест лежащие, следовательно, 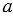
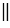
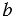 (см. теорему 1). Что и требовалось доказать.
(см. теорему 1). Что и требовалось доказать.
3. Теорема
| Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны. |
Дано: прямые 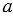 и
и 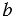 , АВ - секущая,
, АВ - секущая,  1 и
1 и  2 - односторонние,
2 - односторонние,  1 +
1 +  2 = 1800 (Рис.7).
2 = 1800 (Рис.7).
Доказать: 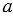
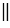
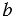 .
.
Доказательство:
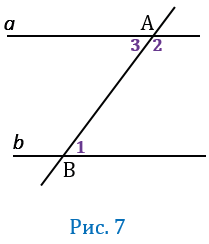
Углы 3 и 2 - смежные, значит по свойству смежных углов  3 +
3 +  2 = 1800, откуда
2 = 1800, откуда  3 = 1800 -
3 = 1800 -  2, при этом
2, при этом  1 +
1 +  2 = 1800, откуда
2 = 1800, откуда  1 = 1800 -
1 = 1800 -  2, тогда
2, тогда  1 =
1 =  3, а углы 1 и 3 накрест лежащие, следовательно,
3, а углы 1 и 3 накрест лежащие, следовательно, 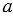
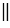
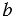 (см. теорему 1). Что и требовалось доказать.
(см. теорему 1). Что и требовалось доказать.
Советуем посмотреть:
Практические способы построения параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Правило встречается в следующих упражнениях:
7 класс
Задание 189, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 588, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 659, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 853, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 484, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 890, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 895, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник