Пропорциональные отрезки в прямоугольном треугольнике
Задача
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Дано:  АВС - прямоугольный,
АВС - прямоугольный,  С - прямой, СD - высота.
С - прямой, СD - высота.
Доказать:  АВС
АВС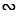
 АСD,
АСD,  АВС
АВС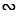
 СВD,
СВD,  АСD
АСD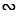
 СВD.
СВD.
Доказательство:
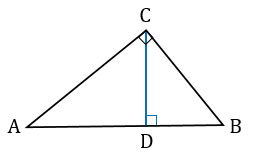
1. В  АВС и
АВС и  АСD:
АСD:  А - общий,
А - общий,  АСВ =
АСВ = АDС = 900, следовательно,
АDС = 900, следовательно,  АВС
АВС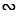
 АСD (по 1 признаку подобия треугольников).
АСD (по 1 признаку подобия треугольников).
2. В  АВС и
АВС и  СВD:
СВD:  В - общий,
В - общий,  АСВ =
АСВ = ВDС = 900, следовательно,
ВDС = 900, следовательно,  АВС
АВС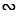
 СВD (по 1 признаку подобия треугольников), поэтому из определения подобных треугольников следует, что
СВD (по 1 признаку подобия треугольников), поэтому из определения подобных треугольников следует, что  АСВ =
АСВ = ВDС.
ВDС.
3. В  АСD и
АСD и  СВD:
СВD:  АСВ =
АСВ = ВDС,
ВDС,  АDС =
АDС = ВDС = 900, следовательно,
ВDС = 900, следовательно,  АСD
АСD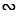
 СВD (по 1 признаку подобия треугольников). Что и требовалось доказать.
СВD (по 1 признаку подобия треугольников). Что и требовалось доказать.
Средним пропорциональным (или средним геометрическим) двух отрезков АВ и СD, называется такой отрезок ХY, что: 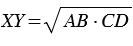 .
.
Утверждения:
|
10. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. |
Доказательство
Дано:  АВС - прямоугольный,
АВС - прямоугольный,  С - прямой, СD - высота, АВ - гипотенуза.
С - прямой, СD - высота, АВ - гипотенуза.
Доказать: 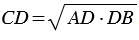 .
.
Доказательство:

 АСD
АСD
 СВD (доказательство данного утверждения приведено в задаче выше), поэтому сходственные стороны данных треугольников пропорциональны, т.е.
СВD (доказательство данного утверждения приведено в задаче выше), поэтому сходственные стороны данных треугольников пропорциональны, т.е. 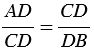 , откуда,
, откуда, 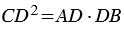 , тогда
, тогда 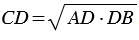 . Что и требовалось доказать.
. Что и требовалось доказать.
| 20. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. |
Доказательство
Дано:  АВС - прямоугольный,
АВС - прямоугольный,  С - прямой, СD - высота, АВ - гипотенуза.
С - прямой, СD - высота, АВ - гипотенуза.
Доказать: 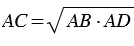 ,
, 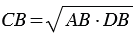 .
.
Доказательство:

1. В  АВС и
АВС и  АСD:
АСD:  А - общий,
А - общий,  АСВ =
АСВ = АDС = 900, следовательно,
АDС = 900, следовательно,  АВС
АВС
 АСD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е.
АСD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е. 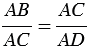 , откуда
, откуда 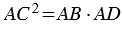 , тогда
, тогда 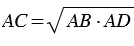 .
.
2. В  АВС и
АВС и  СВD:
СВD:  В - общий,
В - общий,  АСВ =
АСВ = ВDС = 900, следовательно,
ВDС = 900, следовательно,  АВС
АВС
 СВD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е.
СВD (по 1 признаку подобия треугольников), поэтому сходственные стороны данных треугольников пропорциональны, т.е. 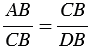 , откуда
, откуда 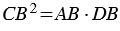 , тогда
, тогда 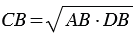 . Что и требовалось доказать.
. Что и требовалось доказать.
Советуем посмотреть:
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Практические приложения подобия треугольников
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Правило встречается в следующих упражнениях:
7 класс
Задание 572, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 573, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 574, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 575, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 577, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 578, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 623, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 668, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 855, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 868, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник