О подобии произвольных фигур

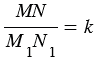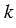Подобные фигуры - это такие фигуры F и F₁, что каждой точке фигуры F можно сопоставить точку фигуры F₁ так, что для любых двух точек М и N фигуры F и сопоставленных им точек М₁ и N₁ фигуры F₁ выполняется равенство , где - одно и то же положительное число для всех точек. При этом предполагается, что каждая точка фигуры F₁ оказывается сопоставленной какой-то точке фигуры F. Число 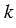называется коэффициентом подобия фигур F и F₁.

Способ построения фигуры, подобной данной

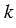
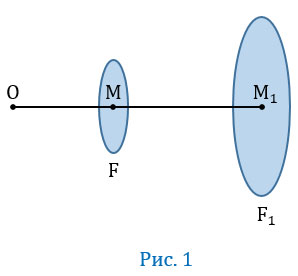
Построим фигуру F₁, подобную фигуре F. Каждой точке М фигуры F сопоставляется точка М₁ плоскости так, что точки М и М₁ лежат на луче с началом в некоторой фиксированной точке О, причем ОМ = ОМ₁. В результате такого сопоставления получается фигура F₁, подобная фигуре F (Рис.1). В таком случае фигуры F и F₁ называются центрально-подобными, а само описанное сопоставление называется центральным подобием или гомотетией.

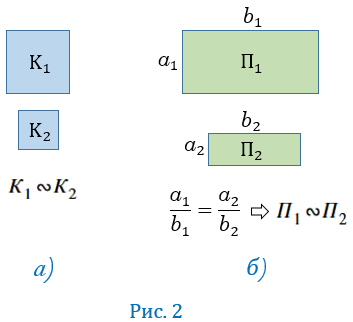
Примерами подобных четырехугольников являются любые два квадрата (рис.2,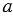), а также два прямоугольника, у которых две смежные стороны одного прямоугольника пропорциональны двум смежным сторонам другого (рис.2, б). Примерами подобных фигур произвольной формы являются две географические карты одного и того же района, но имеющие разный масштаб, а также фотографии одного и того же предмета, сделанные в разных увеличениях.

Замечание

Отношение площадей двух подобных многоугольников равно квадрату коэффициента подобия (также как и отношение площадей двух подобных треугольников).