Построение угла, равного данному

Пример:

Отложить от данного луча угол, равный данному.

Дано: луч ОМ, А.

Отложить: от луча ОМ угол, равный А.

Решение:

Произвольно строим с помощью линейки А и луч ОА.

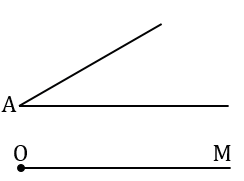
Строим с помощью циркуля окружность произвольного радиуса с центром в вершине А.

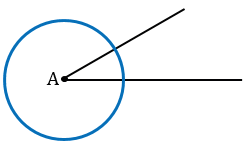
Точки пересечения окружности со сторонами А обозначаем В и С, соединяем их  с помощью линейки.

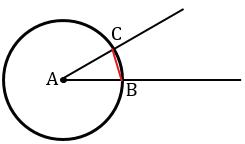
Построим с помощью циркуля окружность того же радиуса, как и окружность с центром в вершине А, от начала луча ОМ точке О.

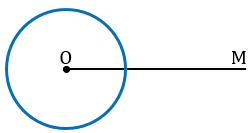
Точку пересечения данной окружности с лучом ОМ обозначим D.

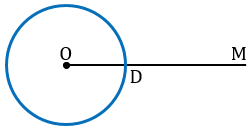
Теперь строим с помощью циркуля окружность радиуса ВС с центром в точке D.

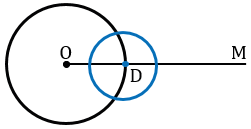
Получаем окружности с центрами в точках О и D пересекаются в двух точках, обозначим одну из этих точек Е.

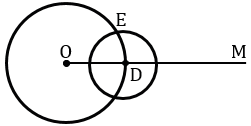
С помощью линейки проведем луч ОЕ.

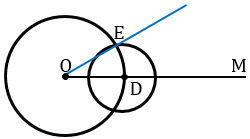
Докажем, что МОЕ - искомый угол, т.е. МОЕ = А.

Рассмотрим треугольники АВС и ОDE.

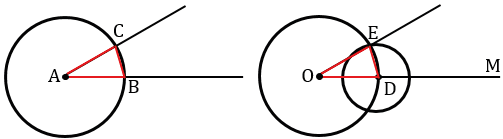
Отрезки АВ и АС - радиусы окружности с центром в точке А, ОD и ОЕ - радиусы окружности с центром в точке О, а по построению эти окружности имеют одинаковые радиусы, следовательно, АВ = ОD, АС = ОЕ. Также по построению радиус DE окружности с центром в точке D равен отрезку ВС, т.е. DE = ВС. Получаем 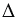АВС =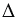ODE по 3 признаку равенства треугольников, следовательно, DОЕ =ВАС, т.е. построенный МОЕ равен данному А (т.к. по рисунку видно, что DОЕ совпадает с МОЕ, а ВАС совпадает с А). Что и требовалось доказать.