Третий признак равенства треугольников

Теорема

Пример:

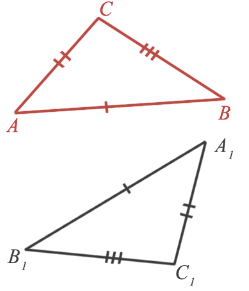
ABC = A₁B₁C₁, так как AC = A₁C₁, AB =A₁B₁ и  BC =B₁C₁.

Из данной теоремы следует, что треугольник - жесткая фигура, т.е. фигура, не подверженная деформации.

Доказательство:

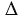Дано: ABC, A₁B₁C₁, AC = A₁C₁, AB =A₁B₁, BC =B₁C₁.

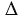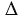Доказать: ABC = A₁B₁C₁

Доказательство:

Приложим 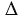ABC к A₁B₁C₁ так, чтобы вершина A совместилась с вершиной A₁, вершина B - с вершиной B₁, а вершины C и C₁ оказались по разные стороны от прямой AB (A₁B₁).

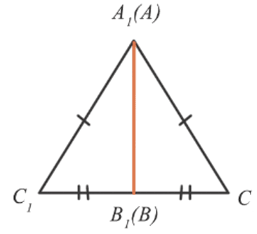
1. Луч CC₁ проходит внутри A₁C₁B₁.

2. Луч CC₁ совпадает с одной из сторон 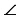A₁C₁B₁.

3. Луч CC₁ проходит вне 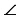A₁C₁B₁.(обратите внимание, что, несмотря на то, что изображения в п.2 и в п.3 похожи, эти два случая для различных треугольников)

Рассмотрим последний случай (остальные доказываются аналогично): Поскольку по условию теоремы AC = A₁C₁, BC =B₁C₁, то CB₁C₁ и 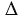CA₁C₁ - равнобедренные. По теореме о свойстве углов равнобедренного треугольника 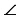B₁CC₁ = 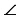B₁C₁C, 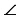A₁CC₁ = 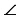A₁C₁C. Следовательно, 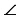B₁CA₁ = 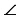B₁C₁A₁ (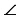B₁CA₁ = 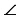B₁CC₁ - 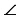A₁CC₁ = 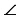B₁C₁C - 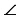A₁C₁C  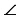= B₁C₁A₁). 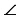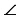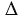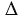Таким образом, AC = A₁C₁, BC = B₁C₁, B₁CA₁ = B₁C₁A₁ , а из этого следует, что ABC = A₁B₁C₁ по I признаку равенства треугольников, что и требовалось доказать.