Среднее пропорциональное
Среднее пропорциональное положительных чисел 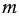 и
и 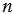 - это такое число
- это такое число 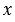 , которое равно квадратному корню из произведения этих чисел, т.е.
, которое равно квадратному корню из произведения этих чисел, т.е. 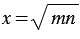 .
.
Среднее пропорциональное носит такое название, потому что число 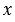 является средним членом пропорции
является средним членом пропорции 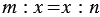 .
.
Средним пропорциональным (или средним геометрическим) двух отрезков 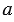 и
и 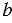 , называется такой отрезок
, называется такой отрезок 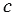 , что:
, что: 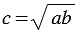 .
.
Чтобы построить среднее пропорциональное двух отрезков используют циркуль и линейку.
Ход построения:
Пусть нам даны два отрезка 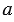 и
и 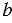 , строим их.
, строим их.
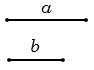
Затем строим с помощью линейки прямую 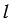 , отмечаем на ней точку А и строим отрезок АЕ, равный отрезку
, отмечаем на ней точку А и строим отрезок АЕ, равный отрезку 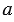 . Для этого строим с помощью циркуля окружность радиуса
. Для этого строим с помощью циркуля окружность радиуса 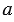 с центром А (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезок ЕВ, равный отрезку
с центром А (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезок ЕВ, равный отрезку 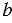 .
.
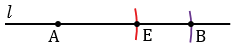
Далее найдем середину отрезка АВ. Для этого строим две окружности с центрами А и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая пересечет отрезок АВ в его середине О.
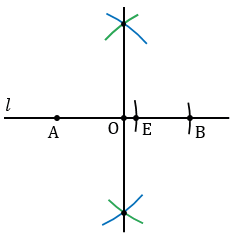
Теперь строим окружность с центром О радиуса ОА.
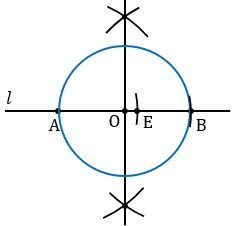
Затем построим перпендикуляр к прямой 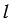 так, чтобы он проходил через точку Е, которая делит отрезок АВ в отношении
так, чтобы он проходил через точку Е, которая делит отрезок АВ в отношении 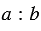 . Для этого строим окружность произвольного радиуса с центром Е (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую
. Для этого строим окружность произвольного радиуса с центром Е (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую 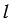 в двух точках М и В (точку В мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центром Е и прямой
в двух точках М и В (точку В мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центром Е и прямой 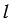 могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центром Е). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой
могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центром Е). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой  и пересечет окружность с центром О в точке К.
и пересечет окружность с центром О в точке К.
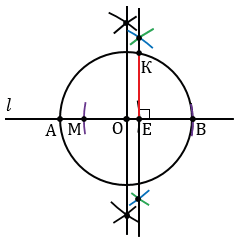
Длина отрезка ЕК и есть искомый отрезок 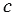 , равный среднему пропорциональному отрезков
, равный среднему пропорциональному отрезков 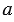 и
и 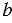 , т.е.
, т.е. 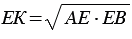 или
или 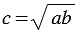 .
.
Советуем посмотреть:
Построение угла, равного данному
Построение перпендикулярных прямых
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник