Упражнение 265 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 91

а) \(2x^2 + 3x - 5 \ge 0\)

\(y = 2x^2 + 3x - 5\) - парабола, ветви которой направлены вверх, так как \(a = 2 > 0\).

\(2x^2 + 3x - 5 = 0\)

\(D = 3^2 - 4\cdot 2 \cdot (-5) =\)

\(=9 + 40 = 49 > 0\) - 2 корня.

\(\sqrt D = 7\).

\(x_{1} = \frac{-3 - 7}{2\cdot 2} = \frac{-10}{4} = -\frac{5}{2} = -2,5\)

\(x_{2} = \frac{-3 + 7}{2\cdot 2} = \frac{4}{4} = 1\)

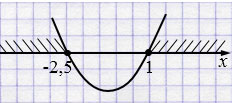
Ответ: \(x \in (-\infty; -2,5] \cup [1; +\infty )\).

б) \(-6x^2 + 6x + 36 \ge 0\)

\(y = -6x^2 + 6x + 36\) - парабола, ветви которой направлены вниз, так как \(a = - 6 < 0\).

\(-6x^2 + 6x + 36 = 0\)

\(D = 6^2 - 4\cdot (-6)\cdot 36 =\)

\(=36 + 864 = 900 > 0\) - 2 корня.

\(x_{1} = \frac{-6 - 30}{2\cdot (-6)} = \frac{-36}{-12} = 3.\)

\(x_{2} = \frac{-6 + 30}{2\cdot (-6)} = \frac{24}{-12} = -2.\)

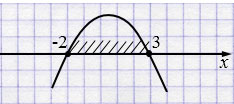
Ответ: \(x \in [-2;\,3]\).

в) \(-x^2 + 5 \le 0\)

\(y = -x^2 + 5\) - парабола, ветви которой направлены вниз, так как \(a = -1 < 0\).

\(-x^2 + 5 = 0\)

\(-x^2 = -5\)

\(x^2 = 5\)

\(x = \pm \sqrt5\)

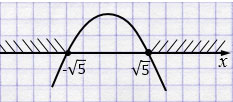
Ответ: \(x \in (-\infty ; -\sqrt5) \cup (\sqrt5; +\infty)\).

Пояснения:

Решение неравенств вида

\(ax^2 + bx + c > 0\) и \(ax^2 + bx + c < 0\):

1) находим дискриминант квадратного трехчлена \(ax^2 + bx + c\) и выясняем имеет ли трехчлен корни;

2) если трехчлен имеет корни, то отмечаем их на оси \(x\) и через отмеченные точки проводим схематически параболу, ветви которой направлены вверх при \(a > 0\) или вниз при \(a < 0\); если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при \(a > 0\) или нижней при \(a < 0\);

3) находят на оси \(x\) промежутки, для которых точки параболы расположены выше оси \(x\) (если решают неравенство \(ax^2 + bx + c > 0\)) или ниже оси \(x\) (если решают неравенство \(ax^2 + bx + c < 0\)).

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

Дискриминант квадратного трехчлена

\(ax^2 + bx + c \):

\(D = b^2 - 4ac\).

Если \(D > 0\), то квадратный трехчлен имеет 2 корня:

\(x_{1,2} = \frac{-b \pm \sqrt D}{2a}\).

Если \(D = 0\), то квадратный трехчлен имеет 1 корень:

\(x = -\frac{b}{2a}\).

Если \(D < 0\), то квадратный трехчлен не имеет корней.

В случае, когда коэффициент \(b = 0\), то есть имеем двучлен \(ax^2 + c\), корни которого: \(x_1 = -\sqrt{\frac{-c}{a}}\) и \(x_2= \sqrt{\frac{-c}{a}}\).