Упражнение 263 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 87
Вернуться к содержанию учебника
Вопрос
В одной системе координат постройте графики функций \(y = x^{2}\) и \(y = x + 6\), с их помощью найдите решение уравнения
\[ x^{2} - x - 6 = 0. \]
Подсказка
Вспомните:
- Квадратичную функцию, ее график.
- Линейную функцию, ее график.
- Координаты точки на координатной плоскости.
Ответ
\[ x^{2} - x - 6 = 0. \]
\[ x^{2} = x + 6. \]
\( y = x^{2} \) - парабола, ветви направлены вверх.
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(9\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) | \(9\) |
\(y = x + 6\) - прямая.
| \(x\) | \(0\) | \(-6\) |
| \(y\) | \(6\) | \(0\) |
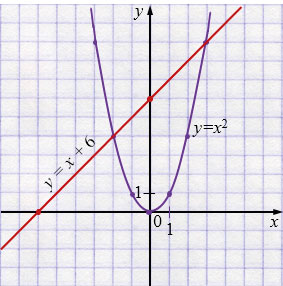
Точки пересечения графиков:
\[ (3;\, 9), \qquad (-2;\, 4). \]
Ответ: корни уравнения
\( x = -2,\; x = 3. \)
Пояснения:
Уравнение \( x^{2} - x - 6 = 0\), выполнив перенос слагаемых с сменой знака, можно записать так: \(x^{2} = x + 6\)
Уравнение вида \(x^{2} = x + 6\) означает, что ищутся такие \(x\), при которых значения квадратичной функции и линейной одинаковы. На графике это точки пересечения параболы \(y = x^{2}\) и прямой \(y = x + 6\). А решением уравнения \(x^{2} = x + 6\) являются значения координаты \(x\) для точек пересечения графиков функций \(y = x^{2}\) и прямой \(y = x + 6\).
Вернуться к содержанию учебника