Упражнение 148 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 56

а) \(5x - 0{,}7 < 3x + 5{,}1\)

\(5x - 3x < 5{,}1 + 0{,}7\)

\(2x < 5{,}8\)   \(/ : 2\)

\(x < 2{,}9.\)

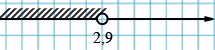
Ответ: \((-\infty; 2,9 ).\)

б) \(0{,}8x + 4{,}5 \ge 5 - 1{,}2x\)

\(0{,}8x + 1{,}2x \ge 5 - 4{,}5\)

\(2x \ge 0{,}5\)    \(/ : 2\)

\(x \ge 0{,}25.\)

Ответ: \([0,25; +\infty).\)

в) \(2x + 4{,}2 \le 4x + 7{,}8\)

\(2x -4x \le 7{,}8-4,2\)

\(-2x \le 3,6\)   \(/ : (-2)\)

 \(x \ge -1{,}8.\)

Ответ: \([-1,8; +\infty).\)

г) \(3x - 2{,}6 > 5{,}5x - 3{,}1\)

\(3x - 5{,}5x > -3{,}1 + 2{,}6\)

\(-2{,}5x > -0{,}5\)    \(/ : (-2,5)\)

\(x < \frac{-0{,}5}{-2{,}5}\)

\(x < 0{,}2.\)

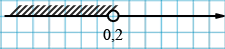
Ответ: \((-\infty; 0,2 ).\)

Пояснения:

При решении рассматриваемых неравенств помним:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.