Упражнение 126 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

Точки пересечения находятся из системы:

\( \begin{cases} y = -x^{2},\\[4pt] y = 2x - 3. \end{cases} \)

\[ -x^{2} = 2x - 3. \]

\( -x^{2} - 2x + 3 = 0 \)       \(\color{red}\times(-1)\)

\[ x^{2} + 2x - 3 = 0\]

\( D =b^2-4ac 2^{2} - 4\cdot1\cdot(-3) =\)

\(=4 + 12 = 16, \)   \(\sqrt{D}=4.\)

\[ x _{1,2}= \frac{-b \pm \sqrt{D}}{2a}. \]

\[ x_1 = \frac{-2 + 4}{2} = \frac{2}{2} = 1. \]

\[ x_2 = \frac{-2 - 4}{2} = \frac{-6}{2} = -3. \]

\[y_1 = -x^{2} = -1^{2} = -1. \]

\[ y_2 = -x^{2} = -(-3)^{2} = -9. \]

Точки пересечения: \((1,\ -1)\) и \((-3,\ -9)\).

\(y = -x^{2}\)

\(y = 2x - 3\)

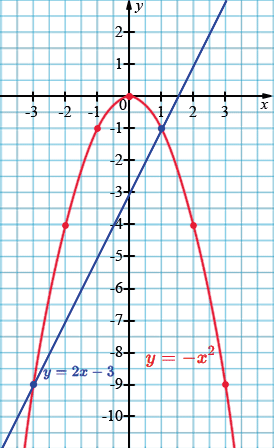
Ответ: точки пересечения — \((1,\ -1)\) и \((-3,\ -9)\).

Пояснения:

— Парабола \(y=-x^{2}\) направлена вниз.

— Прямая \(y=2x-3\) возрастает.

— Точки пересечения — это решения уравнения \(-x^{2} = 2x-3\).

Получаем квадратное уравнение и находим два корня, значит графики пересекаются в двух точках.

Графическая иллюстрация выполняется по точкам:

1) построить параболу \(y=-x^{2}\);

2) построить прямую \(y=2x-3\);

3) отметить точки пересечения: \((1,-1)\) и \((-3,-9)\).

а) \( y = 0{,}5x^{2} - 2 \)

1. Графиком данной функции является парабола, ветви которой направлены вверх \((a = 0{,}5 > 0).\)

2. \( m = -\frac{b}{2a} =-\frac{0}{2\cdot0,5}= 0\),

\(n =0,5\cdot0^2-2= -2. \)

Вершина параболы: \((0;-2)\). Прямая \(x=0\) - ось симметрии параболы.

3.  Нули функции:

\( 0{,}5x^{2} - 2 = 0\)    \(|\times2\)

\( x^{2} - 4 = 0\)

\((x-2)(x+2)= 0\)

\(x-2= 0\)  или \(x+2= 0\)

\(x=2\)                \(x=-2\)

\((2; 0)\) и \((-2; 0)\) - точки пересечения с осью \(x\).

4. Точка пересечения с осью \(y\): \((0; -2)\).

б) \( y = x^{2} - 4x + 4\)

1. Графиком данной функции является парабола, ветви которой направлены вверх \((a=1>0).\)

2. \( m = -\frac{b}{2a} =-\frac{-4}{2\cdot1}= 2\),

\(n = 2^{2} - 4\cdot2 + 4=0\)

Вершина параболы: \((2; 0).\) Прямая \(x=2\) - ось симметрии параболы.

3. Нули функции:

 \( x^{2} - 4x + 4=0\)

\((x-2)^2=0\)

\(x-2=0\)

\(x=2\)

4. Точка пересечения с осью \(y:\)

\(x=0:\) \( y = 0^{2} - 4\cdot0 + 4=4\)

\((0; 4).\)

в) \( y = -x^{2} + 2x \)

1. Графиком данной функции является парабола, ветви которой направлены вниз \((a=-1<0).\)

2. \(m = -\frac{b}{2a} = -\frac{2}{2\cdot(-1)} = 1\)

\(n= -(1)^2 + 2\cdot1 = 1.\)

Вершина параболы: \((1;1)\). Прямая \(x=1\) - ось симметрии параболы.

3. Нули функции:

\(-x^{2} + 2x=0 \)

\(-x(x -2)=0 \)

\(x=0\) или \(x -2=0\)

                   \(x=2\)

\((0; 0)\) и \((2; 0)\) - точки пересечения с осью \(x.\)

4. Точка пересечения с осью \(y\): \((0; 0)\)

Пояснения:

1. Формула вершины параболы \((m; n)\):

\[ m = -\frac{b}{2a},\qquad n = f(m). \]

Это справедливо для любой функции вида \[ y = ax^2 + bx + c. \]

2. Ось симметрии

Ось симметрии — вертикальная прямая: \( x = m\).

3. Направление ветвей

• если \(a > 0\) — ветви вверх;

• если \(a < 0\) — ветви вниз.